


Next: connection
Topics in Non commutative algebraic geometry and
congruent zeta functions (Part IV).
Theory of connections.
Yoshifumi Tsuchimoto
Jujitsu? I'm going to learn Jujitsu?
Neo, ca 2199
In this part we present basic tools of ``differential geometry on schemes.''
Since we mainly deal with local theories, we describe them in terms of
rings and modules.
Even so, students who are interested may note that
the technique employed here (except for last few sections
where the story is specific for characteristic 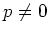 )
is also applicable for ordinary differential geometry.
In fact, for any differentiable manifold
)
is also applicable for ordinary differential geometry.
In fact, for any differentiable manifold 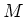 , we have
, we have
- The ring
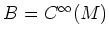 of
of 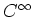 -functions on
-functions on 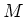 plays the role of ``affine coordinate ring''.
that is, if
plays the role of ``affine coordinate ring''.
that is, if 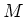 is compact, the set
is compact, the set
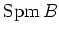 of maximal ideals of
of maximal ideals of 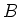 with the Zariski topology is homeomorphic to
with the Zariski topology is homeomorphic to 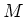 .
If
.
If 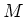 is not compact,
is not compact,
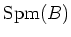 is a bit larger, containing ``ideal boundaries'' of
is a bit larger, containing ``ideal boundaries'' of 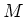 , but even then
, but even then 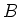 carries virtually all the information to study
carries virtually all the information to study 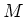 .
.
- The Lie algebra of derivations
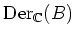 is
identified with the Lie algebra of
is
identified with the Lie algebra of 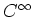 vector field on
vector field on 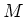 .
.
- The module of 1-forms
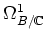 is identified with the
module of
is identified with the
module of 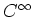 -1-forms over
-1-forms over 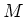 .
.
And so on. So the theory here gives results on differential manifold
without serious modifications.



Next: connection
2007-12-26
![]() )
is also applicable for ordinary differential geometry.
In fact, for any differentiable manifold
)
is also applicable for ordinary differential geometry.
In fact, for any differentiable manifold ![]() , we have
, we have