exterior derivation

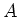Let $A$ be a commutative ring. Let 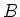$B$ be a commutative 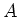$A$ -algebra. We have already defined the exterior derivation

$$d:B\to \Omega^1_{B/A}.$$

We define

$$\Omega^\bullet_{B/A}=\wedge_{B} \Omega^1_{B/A}.$$

²

We would like to extend this to a map

$$d:\Omega^\bullet_{B/A} \to \Omega^\bullet_{B/A}$$

which satisfies the following rules.

$$d^2=0$$ (EXT1)

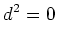$$d(\alpha\wedge \beta)=(d\alpha)\wedge \beta + (-1)^k\alpha\wedge ... ...d (\forall \alpha \in \Omega^k_{B/A} ,\forall \beta \in \Omega^\bullet_{B/A})$$ (EXT2)

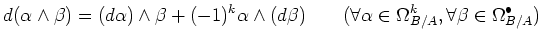It is easy to see that 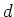$d$ is uniquely determined by the