

Next: Lie derivation
Up: some linear algebra
Previous: pairing of exterior algebras
We employ the same assumption of the previous subsection.
For any 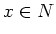 , we define
, we define
to be the unique 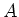 -linear map which satisfies the following properties.
-linear map which satisfies the following properties.
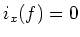 for any
for any 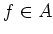 .
.
-
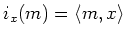 for any
for any 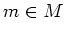 .
.
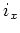 is an odd derivation. That means,
is an odd derivation. That means,
The proof of the well-definedness of 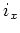 is similar to the proof of
well-definedness of
is similar to the proof of
well-definedness of 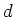 . We leave the detail to the reader.
. We leave the detail to the reader.
Using the above definition
we may also explicitly write down a formula for the interior derivations.
This leads to an important adjunction relation
(We may verify the above equation by using the
``determinant expansions by minors''.)
In particular, we note that for any 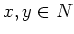 , an anti commutation relation
, an anti commutation relation
holds. Another useful equation is


Next: Lie derivation
Up: some linear algebra
Previous: pairing of exterior algebras
2007-12-26
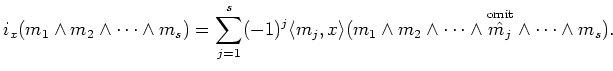
![]() , an anti commutation relation
, an anti commutation relation