

Next: 微分方程式
Up: 自然対数の底 e
Previous: 指数関数の微分
前節で、
という関数を導入したが、これは実は対数関数なのだ。
この節ではそのことを示そう。
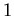 より大きい正の数
より大きい正の数 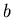 をとって、とりあえず固定しておく。
正の実数
をとって、とりあえず固定しておく。
正の実数  を任意にとり、
を任意にとり、
ということに着目する。
上の式の両辺を 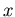 で微分し、
で微分し、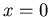 とおくと、
とおくと、
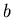 を止めて
を止めて  を動かすと、
を動かすと、 は
は  の関数として
の関数として
 の定数倍であることがわかる。
対数関数のいくつかの性質を思い出せば、
これで前々節保留しておいた
の定数倍であることがわかる。
対数関数のいくつかの性質を思い出せば、
これで前々節保留しておいた 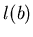 の性質が確かめられたことになる。
の性質が確かめられたことになる。
さらに、
であることもついでにわかったわけである。
Yoshifumi Tsuchimoto
2000-04-12
