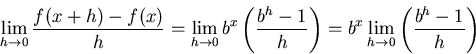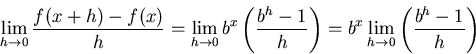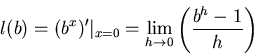

Next: の正体
Up: 自然対数の底 e
Previous: 自然対数の底 e
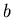 は正の実数とする。
は正の実数とする。 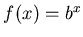 の微分を考えてみよう。
の微分を考えてみよう。
だから、
の部分がわかればいい。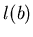 が存在することは他の本を眺めて頂くことにして、
ここでは、
が存在することは他の本を眺めて頂くことにして、
ここでは、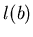 は
は 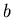 について単調増加で、
について単調増加で、
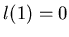 ということのみに注意することにしよう。
さらに、
ということがわかれば、
ということのみに注意することにしよう。
さらに、
ということがわかれば、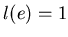 となる正の数
となる正の数 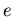 がただ一つあることがわかって、
この
がただ一つあることがわかって、
この 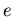 に関する指数関数は微分に関して特別に簡単な形、すなわち
に関する指数関数は微分に関して特別に簡単な形、すなわち
を持つことがわかる。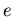 のことを自然対数の底という。
のことを自然対数の底という。
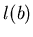 に関する上記の二つのことを
に関する上記の二つのことを 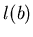 の定義から直接示すこともできる。
しかし、それはわざとらしい感じがするので、
次節で
の定義から直接示すこともできる。
しかし、それはわざとらしい感じがするので、
次節で 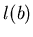 の正体をばらし、
上の二つのことを示そう。
の正体をばらし、
上の二つのことを示そう。
Yoshifumi Tsuchimoto
2000-04-12