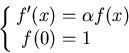

Next: 三角関数とその一次結合の満たす微分方程式
Up: 自然対数の底 e
Previous: の正体
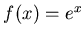 は、微分しても変わらない、つまり、
は、微分しても変わらない、つまり、
を満たすことがわかりました。
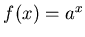 は、
は、
(
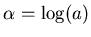 )をみたします。
逆に、このような性質を満たす関数がどのぐらいあるかを
調べてみましょう。(このような、微分の満たす関係式を、微分方程式、と言い、
そこから元の関数を求めることを微分方程式を解くと言ったりします。)
)をみたします。
逆に、このような性質を満たす関数がどのぐらいあるかを
調べてみましょう。(このような、微分の満たす関係式を、微分方程式、と言い、
そこから元の関数を求めることを微分方程式を解くと言ったりします。)
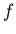 が関係式を満たすとし、それと
が関係式を満たすとし、それと
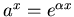 との違いをみたいわけです。
ここでは、
との違いをみたいわけです。
ここでは、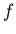 を
を
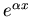 で割った
で割った
を調べてみることにします。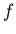 のところを
のところを
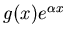 で置き換えることによって、
で置き換えることによって、
が得られることがわかるでしょう。
微分して 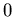 ということは、
ということは、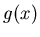 のグラフの接線が
常に
のグラフの接線が
常に 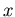 軸と平行ということですから、
軸と平行ということですから、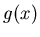 は定数(仮に
は定数(仮に 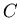 とおく)です。
とおく)です。
となって、もくろみどおり 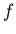 は
は 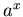 と定数倍の違いしかない
ということがわかりました。簡単にわかるように、
と定数倍の違いしかない
ということがわかりました。簡単にわかるように、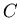 がどんな値であっても
がどんな値であっても
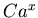 は元の微分方程式を満たします。もし
は元の微分方程式を満たします。もし 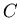 の値までこめて込めて
決定できるような方程式系を作りたいなら、例えば、
の値までこめて込めて
決定できるような方程式系を作りたいなら、例えば、
などというように指定してやるのが良いでしょう。
Yoshifumi Tsuchimoto
2000-04-12