

Next: 偏角を選ぶことの面倒な点
Up: 対数関数の多価性について
Previous: 偏角を一意に決めてみる。
前小節のように、複素数の偏角を 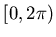 (あるいは、
(あるいは、
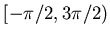 など)
の範囲に決め打ちれば、関数
など)
の範囲に決め打ちれば、関数 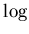 を一価にすることが出来る。
そこで、この節以降では、対数関数の実関数による表現
を一価にすることが出来る。
そこで、この節以降では、対数関数の実関数による表現
の、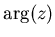 の範囲を
の範囲を 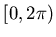 に制限して、
に制限して、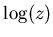 を一価関数
にしたものを
を一価関数
にしたものを
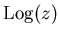 と書くことにする。
この新しい
と書くことにする。
この新しい
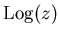 は実数に対する「通常の」対数関数の拡張になっている。
すなわち、
は実数に対する「通常の」対数関数の拡張になっている。
すなわち、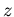 が実数ならば
が実数ならば
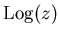 は今までに定義した通常の対数関数に
一致する。
は今までに定義した通常の対数関数に
一致する。
Yoshifumi Tsuchimoto
2000-04-12