

Next: 対数関数を一価関数にしてみる。
Up: 対数関数の多価性について
Previous: 対数関数の多価性について
対数関数の計算式
において、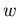 の「偏角」
の「偏角」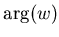 を一意に決めずに、
を一意に決めずに、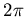 の整数倍
の分の不定性を許していたのが
の整数倍
の分の不定性を許していたのが 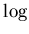 の多価性の原因であったと考えられる。
の多価性の原因であったと考えられる。
では、しばしばやるように、
とすれば良いのではなかろうか。
確かに、このように決めてしまえば 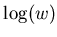 は (☆)式によって
一意に定まり、いちいち多価性に気をつけなくても済む。
前前節の 「
は (☆)式によって
一意に定まり、いちいち多価性に気をつけなくても済む。
前前節の 「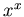 」のグラフにしても、分枝をいくつも書かずに
一つだけ書けば済んだのである。
」のグラフにしても、分枝をいくつも書かずに
一つだけ書けば済んだのである。
偏角を 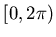 の中に選ぶことにすると、「境目」である偏角=0 の部分が
ちょうど実軸上に来てうっとうしいと思われる向きには、偏角を
の中に選ぶことにすると、「境目」である偏角=0 の部分が
ちょうど実軸上に来てうっとうしいと思われる向きには、偏角を
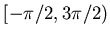 の中に選ぶなどの方法をとることも出来る。
そうすると選ぶ分枝は変わってしまうが、
分枝を一つだけ考えれば済むという点ではかわらない。
の中に選ぶなどの方法をとることも出来る。
そうすると選ぶ分枝は変わってしまうが、
分枝を一つだけ考えれば済むという点ではかわらない。
Yoshifumi Tsuchimoto
2000-04-12
![]() の中に選ぶことにすると、「境目」である偏角=0 の部分が
ちょうど実軸上に来てうっとうしいと思われる向きには、偏角を
の中に選ぶことにすると、「境目」である偏角=0 の部分が
ちょうど実軸上に来てうっとうしいと思われる向きには、偏角を
![]() の中に選ぶなどの方法をとることも出来る。
そうすると選ぶ分枝は変わってしまうが、
分枝を一つだけ考えれば済むという点ではかわらない。
の中に選ぶなどの方法をとることも出来る。
そうすると選ぶ分枝は変わってしまうが、
分枝を一つだけ考えれば済むという点ではかわらない。