![]() のときには、
のときには、![]() の代わりに標準的な
の代わりに標準的な
![]() を
使うことができ、それが本編で述べた
を
使うことができ、それが本編で述べた ![]() である。
以下、区別のために、
である。
以下、区別のために、![]() と言えばこの本来のものを指すことにし、上の
拡張された意味の 「
と言えばこの本来のものを指すことにし、上の
拡張された意味の 「![]() 」を
」を ![]() と書いておくことにする。
と書いておくことにする。
![]() のときでも、
のときでも、![]() として別のものを採用することもできる。
たとえば、
として別のものを採用することもできる。
たとえば、![]() として、
として、
![]() を採用すると、
を採用すると、
![]() の多価性を考慮すると、整数
の多価性を考慮すると、整数 ![]() の一つ一つにたいして、
の一つ一つにたいして、
グラフは次の節を参照して頂きたい。
![]() の時を調べるために、
の時を調べるために、
![]() と置き直してみる。
と置き直してみる。
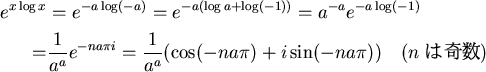
と書き直すことができる。
どの ![]() を採用するかによって、いろいろなグラフになる。
次節でそれらのグラフを書いてみることにする。
を採用するかによって、いろいろなグラフになる。
次節でそれらのグラフを書いてみることにする。