

Next: 対数関数の多価性
Up: 対数関数の定義
Previous: 正の実数の
実数 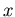 に対して、
に対して、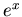 は必ず正の値をとるから、例えば負の数の
は必ず正の値をとるから、例えば負の数の
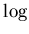 は実数になると期待するわけにはいかない。
そこで、前節に述べたようにまず指数関数を複素数の範囲にまで拡張して考え、
その逆関数として対数関数を考えてみたい。
は実数になると期待するわけにはいかない。
そこで、前節に述べたようにまず指数関数を複素数の範囲にまで拡張して考え、
その逆関数として対数関数を考えてみたい。
そこで、ここではまず対数関数を既知の実関数で表示することを目標にしてみよう。
いま、
という関係式が成り立っていたとする。
我々はこの 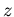 を
を 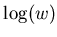 と書きたいのであるが、
ただ書くだけでは全く掴みどころがない。
と書きたいのであるが、
ただ書くだけでは全く掴みどころがない。
そこで、 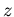 は
は 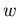 からどうやって計算すれば良いのかという点について、
実関数の知識の範囲内で理解したいのである。
からどうやって計算すれば良いのかという点について、
実関数の知識の範囲内で理解したいのである。
まず、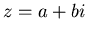 と
と 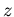 を実部と虚部とにわけ、
を実部と虚部とにわけ、
と書いてみる。両辺の絶対値を比較することにより、
ここで、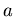 は実数で、しかも
は実数で、しかも 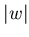 は正の数であると言うことから、
は正の数であると言うことから、
と、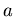 は前小節で述べた道標的な対数関数を使ってあらわすことができる。
これで
は前小節で述べた道標的な対数関数を使ってあらわすことができる。
これで 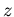 の実部に関してははっきりした。
の実部に関してははっきりした。
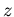 の虚部についてはどうだろうか。(☆)式を見、さらに複素数のガウス平面での
表示についての知識を援用すると、
の虚部についてはどうだろうか。(☆)式を見、さらに複素数のガウス平面での
表示についての知識を援用すると、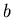 は
は 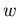 の偏角、すなわち
ベクトル
の偏角、すなわち
ベクトル 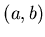 と
と 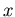 軸とのなす角の角度であるということがわかる。
軸とのなす角の角度であるということがわかる。
よって、
という式が得られ、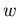 から
から 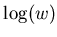 を計算する方法が
わかったことになる。
を計算する方法が
わかったことになる。
Yoshifumi Tsuchimoto
2000-04-12
![]() は
は ![]() からどうやって計算すれば良いのかという点について、
実関数の知識の範囲内で理解したいのである。
からどうやって計算すれば良いのかという点について、
実関数の知識の範囲内で理解したいのである。
![]() と
と ![]() を実部と虚部とにわけ、
を実部と虚部とにわけ、
![]() の虚部についてはどうだろうか。(☆)式を見、さらに複素数のガウス平面での
表示についての知識を援用すると、
の虚部についてはどうだろうか。(☆)式を見、さらに複素数のガウス平面での
表示についての知識を援用すると、![]() は
は ![]() の偏角、すなわち
ベクトル
の偏角、すなわち
ベクトル ![]() と
と ![]() 軸とのなす角の角度であるということがわかる。
軸とのなす角の角度であるということがわかる。