

Next: この節のまとめ
Up: 対数関数の定義
Previous: 指数関数の逆関数としての
という式が得られ、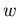 から
から 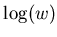 を計算する方法が
わかって、めでたしめでたし、というところだが、
実は問題がある。それは
を計算する方法が
わかって、めでたしめでたし、というところだが、
実は問題がある。それは 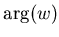 の部分で、
これには
の部分で、
これには 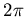 の整数倍の分だけ不定性がある。
すなわち、
の整数倍の分だけ不定性がある。
すなわち、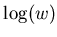 には、
には、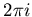 の整数倍の分だけ不定性があるのだ。
の整数倍の分だけ不定性があるのだ。
この不定性は 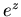 の周期性によるもので、たとえば、
の周期性によるもので、たとえば、
が成り立つから、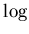 を
を 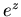 の逆関数として定義する限りは
やむを得ないことであるともいえる。
の逆関数として定義する限りは
やむを得ないことであるともいえる。
しかし、現代数学においては、単に「関数」と言えば一価なもののみをさすから、
ここの点は少しなんとかしなければならない。
さしあたって、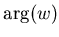 は
は 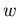 の偏角を「うまく」選んでしのぐことにする。
の偏角を「うまく」選んでしのぐことにする。
Yoshifumi Tsuchimoto
2000-04-12
![]() の周期性によるもので、たとえば、
の周期性によるもので、たとえば、
![]() は
は ![]() の偏角を「うまく」選んでしのぐことにする。
の偏角を「うまく」選んでしのぐことにする。