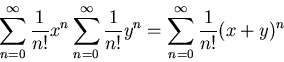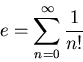

Next: この節のまとめ
Up: 指数関数の巾級数による定義
Previous: この級数の収束の速さ
二番目に注意したいことは、上の巾級数が乗法について良い性質を持つ
ということである。実際、分配法則を何回も使うと、
がわかる。
(上の等式は無限和の間の関係なので、
実際にはもっと注意深く議論しなければならない。
とはいえ前述のようにこれらの巾級数は収束が著しく速いので
扱いはそれほど難しくない。)
この等式 2.3 こそ、この巾級数が正の数の巾乗の性質
と同じ性質を持つことの証明であり、この性質と連続性の議論、それに、
という 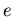 の性質を併用することによって、
ここに巾級数として定義したものが前節の
の性質を併用することによって、
ここに巾級数として定義したものが前節の 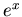 と一致することを
示すことができる。
と一致することを
示すことができる。
Yoshifumi Tsuchimoto
2000-04-12