マニアックには前節のような話があるにしても、 普通は指数関数と言えば連続になるように 定義するのが歴史的にも正統だし、考えとして自然でもあるだろう。 (最近流行りのフラクタル理論などでは、そうともいえないかもしれないが、 悪の私としてはそこら辺は口をつぐんでおくことにする。)
つまり、「![]() は、
は、![]() に近い有理数
に近い有理数 ![]() をとって、
をとって、 ![]() を計算したものの、
を計算したものの、
![]() のときの極限」、記号で書けば
のときの極限」、記号で書けば
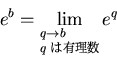
(★)
「![]() が十分
が十分 ![]() に近づくとき、その近付き方に関係なく
に近づくとき、その近付き方に関係なく
![]() はある一定の値に近付く。」
はある一定の値に近付く。」
ということを確かめなければならない。これも詳細は皆さんにお任せしよう。 (次の節も参照して欲しい。)
(★)のような議論を効率良くやるための道具が、よく 《
![]() 論法》
とか呼ばれるもので、大学初年級の学生にとって難関の一つになっている。
でも、これをやっておけば前節のような混乱を避けることができる、
と思えば、便利なものだと言えるのではないだろうか。
論法》
とか呼ばれるもので、大学初年級の学生にとって難関の一つになっている。
でも、これをやっておけば前節のような混乱を避けることができる、
と思えば、便利なものだと言えるのではないだろうか。