

Next: 正の数の無理数乗(正調編)
Up: 指数関数を簡単な場合からコツコツと定義していく
Previous: 正の数の有理数乗
実は、「指数法則」をみたしつつ、「巾指数」について連続ではないような「疑似指数」
を定義することも可能だ。
すこし良く知っている人のためにこの小節で
そのことについて付け加えておこう。
この小節の内容は以下では使われないので、
特に興味のない人は飛ばしてください。
上に述べたような「疑似指数」
は例えば以下の手順で作ることができる。
- 1.
-
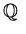 -ベクトル空間としての
-ベクトル空間としての
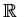 の基底
の基底
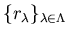 をとって、
をとって、
と直和分解する。
- 2.
- 上の直和分解の直和因子のぶんだけの正の実数の族
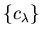 を
選んでおく。
を
選んでおく。
- 3.
- 実数
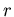 をこの直和分解によって
をこの直和分解によって
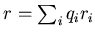 と書く。
と書く。
- 4.
-
と定義する。
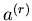 は次のような「指数法則」を満足することがわかる。
は次のような「指数法則」を満足することがわかる。
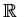 の直和分解と
の直和分解と
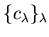 の選びかたをもう少しだけ工夫すれば、
の選びかたをもう少しだけ工夫すれば、
も成り立つようにできる。
Yoshifumi Tsuchimoto
2000-04-12