

Next: 正の数の無理数乗その1(チャチャ編)
Up: 指数関数を簡単な場合からコツコツと定義していく
Previous: 指数関数を簡単な場合からコツコツと定義していく
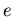 の整数乗はかけ算を繰り返すことにより簡単に定義できる。
の整数乗はかけ算を繰り返すことにより簡単に定義できる。
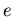 の有理数乗については、3.4 節で述べたような問題があるけれども、
基本的には 3.5 節のように定義すれば良い。つまり、
の有理数乗については、3.4 節で述べたような問題があるけれども、
基本的には 3.5 節のように定義すれば良い。つまり、
ただし、
![$\sqrt[m]{e}$](img81.png) は
は 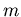 乗して
乗して 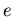 になるような正の
数である。有理数
になるような正の
数である。有理数 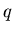 を
を 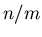 という風に書く方法は (
という風に書く方法は (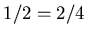 のように)
無限にあって、その書き方によらずに
のように)
無限にあって、その書き方によらずに 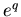 が定義される
ことを示す必要がある。(3.4節で見たように、一見当り前に見えることでも
一度確かめておくことを怠ると、間違いをおかす可能性があるから、あなどれない。)
ここでは、
「一般に、正の数
が定義される
ことを示す必要がある。(3.4節で見たように、一見当り前に見えることでも
一度確かめておくことを怠ると、間違いをおかす可能性があるから、あなどれない。)
ここでは、
「一般に、正の数 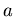 に対して、
に対して、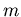 乗して
乗して 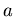 になる正の数は
ただ一つしか無い」ということが、キーポイントなのだ。詳細は
皆さんにお任せしよう。(中間値の定理なんかが、重宝するかも知れない。)
になる正の数は
ただ一つしか無い」ということが、キーポイントなのだ。詳細は
皆さんにお任せしよう。(中間値の定理なんかが、重宝するかも知れない。)
上の定義は指数法則が成り立つようにさだめられたもので、
指数法則を満たすように 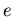 の有理数乗を定義し、
しかも
の有理数乗を定義し、
しかも 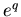 が正の値をとるように要請しようとすると、
その定義は必然的にこうなる。しかし、
が正の値をとるように要請しようとすると、
その定義は必然的にこうなる。しかし、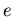 の実数乗を定義しようとする
さいには、別の注意が必要になる。それを次の小節で述べることにしよう。
の実数乗を定義しようとする
さいには、別の注意が必要になる。それを次の小節で述べることにしよう。
Yoshifumi Tsuchimoto
2000-04-12
![]() の整数乗はかけ算を繰り返すことにより簡単に定義できる。
の整数乗はかけ算を繰り返すことにより簡単に定義できる。
![]() の有理数乗については、3.4 節で述べたような問題があるけれども、
基本的には 3.5 節のように定義すれば良い。つまり、
の有理数乗については、3.4 節で述べたような問題があるけれども、
基本的には 3.5 節のように定義すれば良い。つまり、
![]() の有理数乗を定義し、
しかも
の有理数乗を定義し、
しかも ![]() が正の値をとるように要請しようとすると、
その定義は必然的にこうなる。しかし、
が正の値をとるように要請しようとすると、
その定義は必然的にこうなる。しかし、![]() の実数乗を定義しようとする
さいには、別の注意が必要になる。それを次の小節で述べることにしよう。
の実数乗を定義しようとする
さいには、別の注意が必要になる。それを次の小節で述べることにしよう。