

Next: この節のまとめ
Up: 指数関数を簡単な場合からコツコツと定義していく
Previous: 正の数の無理数乗(正調編)
筆者も受験のころには変な値も覚えさせられたもので、
なんていうのも覚えた。
でも、もし、例えば、《
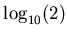 の値を小数第1位まで計算せよ》
という問題が試験に出たとしたら、「覚えているから、これでいーのだ。」
などという理屈は通用しそうにない。
の値を小数第1位まで計算せよ》
という問題が試験に出たとしたら、「覚えているから、これでいーのだ。」
などという理屈は通用しそうにない。
ということを示せば、とりあえず小数第一位までは求まったことになる。
では
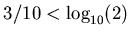 を示すには?
ここまで来ればもうお分かりだろう。
を示すには?
ここまで来ればもうお分かりだろう。
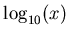 は
は 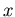 について単調増加
だから、
について単調増加
だから、
を示せば良い。さらにこれを示すには、両辺十乗して、
に帰着すればいい。
ということで、解答は次のようになる。
(解答)
だから、辺々の 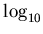 をとって、
をとって、
ゆえに、
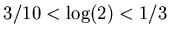 ....
....
結局、指数や対数の定義に戻れば、それなりに計算できるということ。
本節に出て来る話の、特に大きさの評価に関する部分もこのようにして
理解することができる。
Yoshifumi Tsuchimoto
2000-04-12