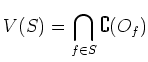
closed subsets

DEFINITION 1.13   Let $A$ be a commutative ring. Let $S$ be a subset of $A$ . Then we define $V(S)$ as follows.

$$V(S)=\bigcap_{f\in S} \complement(O_f)$$

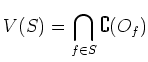
It is a closed subset of $\operatorname{Spec}(A)$ .

LEMMA 1.14   Let $A$ be a commutative ring. Then for any subset $S$ of $A$ , we have the following.

1. $$V(S)=\{ x \in \operatorname{Spec}(A); \rho_x(f)=0 \forall f \in S\}$$

2. $V(S)=V(I)$ where $I=A.S$ is the ideal of $A$ generated by $S$ .

3. $$V(I)=\{x \in \operatorname{Spec}(A); I\subset x\}$$

PROOF.. clear from the definition. $\qedsymbol$

Thus a closed set in $\operatorname{Spec}(A)$ is of the form $V(I)$ for some ideal $I$ .

LEMMA 1.15   For any ideals $I,J$ of a commutative ring $A$ , we have the following.

1. $V(I+J)=V(I)\cap V(J)$ .
2. $V(I J)=V(I)\cup V(J)$ .
3. $V(I)=\emptyset \iff I=A$ .
4. $V(I)=\operatorname{Spec}(A) \iff$   any element of $I$ is nilpotent.

PROOF.. (3): if $I\subsetneq A$ , then by the Zorn's lemma we obtain a maximal ideal $\mathfrak{m}$ which contains $I$ . Since maximal ideals are prime, we have

$$V(I)\ni \mathfrak{m}.$$

Thus $V(I)$ is not empty. The converse is obvious.

(4)is a consequence of Lemma 1.11. $\qedsymbol$

The reader may easily see that the compactness of $\operatorname{Spec}(A)$ (Theorem 1.12) is proved in a more easier way if we have used the terms of closed sets and ``finite intersection property''.

The author cannot help but mentioning little more how the topology of $\operatorname{Spec}(A)$ and the structure of $A$ related to each other.

Though the following statements may never be used in this talk (at least in the near future), we would like to record the statement and its proof.

THEOREM 1.16   Let $A$ be a ring.

1. Assume $\operatorname{Spec}(A)$ is not connected so that it is divided into two disjoint closed sets $V(I)$ and $V(J)$ .
   $$\operatorname{Spec}(A)=V(I)\cup V(J),\quad V(I)\cap V(J)=\emptyset.$$
   Then we have elements $p_1,p_2\in A$ such that
   1. $p_1^2=p_1, p_2^2=p_2, p_1+p_2=1$
   2. $A$ is a product of algebras $A p_1$ , $A p_2$
   3. $\rho_x(p_1)=1$ for all $x\in V(J)$ .
   4. $\rho_x(p_1)=0$ for all $x\in V(I)$ .
2. Conversely, if the ring $A$ has elements $p_1,p_2$ which satisfy (a)-(b) above, then $\operatorname{Spec}(A)$ is divided into two disjoint closed sets.

PROOF.. (1) Since $V(I)$ and $V(J)$ is disjoint, we have

$$V(I+J)=V(I)\cap V(J)=\emptyset$$

Thus $I+J=A$ . It follows that there exists $a_1\in I$ and $a_2\in J$ such that $a_1+a_2=1$ . On the other hand,

$$V(I J)=V(I)\cup V(J)=\operatorname{Spec}(A)$$

implies that any element of $I J$ is nilpotent. Let $N$ be a positive integer such that

$$(a_1a_2)^N=0$$

holds. Then by expanding the equation

$$(a_1+a_2)^{2 N}=1,$$

we obtain an equation of the following form

$$u_1 a_1^N +u_2 a_2^N=1 \qquad(\exists u_1,u_2 \in A)$$

Indeed, we have

$$\sum_{j=N+1}^{2 N} \left( \binom{2 N}{j} a_1^{j-N} a_2^{2 N -j} ... ...N +\sum_{j=0}^{N-1} \left( \binom{2 N}{j} a_1^j a_2^{ N -j} \right) a_2^N =1.$$

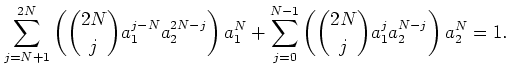
Now let us put $p_1=u_1 a_1^N, p_2=u_2 a_2^N$ . They satisfy

$$p_1+p_2=1,\quad p_1 p_2=0,\quad p_1\in I,\quad p_2 \in J.$$

Then it is easy to verify that the elements $p_1,p_2$ satisfy the required properties. The converse is easier and is left to the reader. $\qedsymbol$