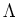PROOF..
Assume
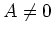
.
Then by Zorn's lemma we always have a maximal ideal
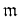
of
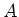
.
A maximal ideal is a prime ideal of
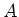
and is therefore an element of
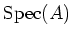
.
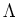
PROOF..
We have already seen that
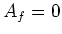
if and only if
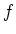
is nilpotent.
(Corollary
1.9).
Since
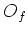
is homeomorphic to
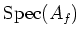
, we have the desired result.