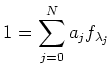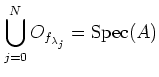PROOF..
Let
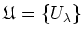
be an open covering of
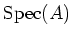
.
We want to find a finite subcovering of
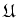
.
For any
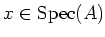 , we have a index
, we have a index 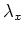 and an
open subset
and an
open subset 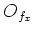 of
of
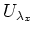 such that
such that
holds. Replacing
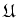
by
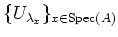
if necessary,
we may assume each
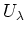
is of the form
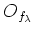
for some
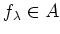
.
Now,
implies that
Now we would like to show from this fact that the ideal
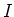
defined by
is equal to
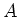
. Assume the contrary. Using Zorn's lemma we may always
obtain an maximal ideal
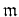
of
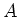
which contains
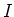
.
This is a contradiction to the fact mentioned above.
Thus we have proved that 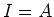 . In particular, we may find a relation
. In particular, we may find a relation
for some positive integer
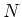
, index sets
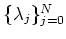
,
and elements
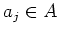
. This clearly means that
as required.
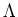
![]() , we have a index
, we have a index ![]() and an
open subset
and an
open subset ![]() of
of
![]() such that
such that
![]() . In particular, we may find a relation
. In particular, we may find a relation