

Next: Abstract Jordan Chevalley decomposition
Up: generalities in finite dimensional
Previous: Semi direct products of
DEFINITION 5.58
Let

be a Lie algebra over a field
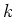
.
Let
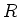
be the radical of

.
A
Levi-subalgebra of

is a
subalgebra
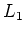
of

such that

is a direct sum of
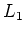
and
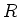
as a vector space over
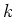
.
We have the following obvious lemma.
LEMMA 5.59
Let  be a Lie algebra over a field
be a Lie algebra over a field 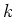 .
Let
.
Let 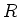 be the radical of
be the radical of  .
Let
.
Let 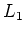 be a Levi-subalgebra of
be a Levi-subalgebra of  .
Then:
.
Then:
-
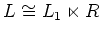 .
.
-
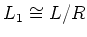 .
.
In particular the isomorphism class of 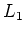 is unique.
is unique.
PROOF..
(1):follows from the general theory.
(2),(3),(4):follows easily from the definition of 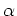 .
.
(5):
For any 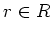 and for any
and for any
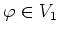 , we have
, we have
(6):
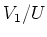 is an
is an 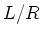 -module which has
-module which has 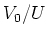 as
a submodule of codimension
as
a submodule of codimension 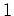 .
Thus by using
Lemma 5.51
(Weyl's theorem on irreducibility (codimension
.
Thus by using
Lemma 5.51
(Weyl's theorem on irreducibility (codimension 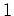 case)),
we see that there exists a 1-dimensional
case)),
we see that there exists a 1-dimensional 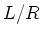 -submodule
-submodule 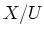 of
of 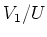 (where
(where 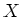 is a
is a  submodule of
submodule of  )
such that
)
such that
holds. Since
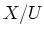
is
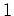
dimensional, the action of the semisimple Lie
algebra
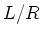
on
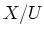
is
trivial. Thus we see that
there exists an element
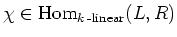
such that
holds.
(7): Since 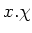 belongs to
belongs to 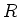 , we know the existence of
, we know the existence of 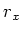 .
The uniqueness of the
.
The uniqueness of the 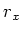 follows from the assumption that the center of
follows from the assumption that the center of  is trivial.
is trivial.
(8),(9): easy.
LEMMA 5.61
Let 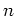 be a positive integer.
Let
be a positive integer.
Let  be an
be an 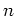 -dimensional Lie algebra over a field
-dimensional Lie algebra over a field 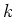 of
characteristic
of
characteristic
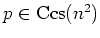 .
Assume
.
Assume
- The radical
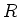 of
of  is abelian.
is abelian.
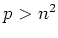 or
or 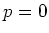 .
.
Then  has a Levi subalgebra.
has a Levi subalgebra.
PROOF..
Let
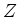
be the center of

.
Applying the previous lemma to
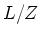
,
We see that there exists an Levi subalgebra
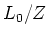
of
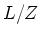
.
Now
is a short exact sequence of
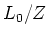
-module, and so it therefore splits.
(Theorem
5.53
(Weyl's theorem of irreducibility.))
Thus
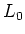
has a subalgebra
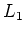
which is stable under action of
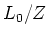
.
That means,
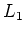
is a Levi subalgebra of
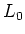
.
So
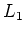
is also a Levi subalgebra of

.
PROOF..
If
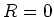
, then we only need to set
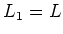
. So let us assume
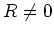
.
Let us put
Then from the definition, we
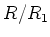
is an abelian Lie algebra.
It is also easy to verify that
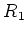
is an ideal of

.
(
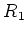
is a
characteristic ideal of
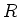
).
We apply the preceding lemma for
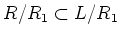
to obtain a Levi subalgebra
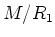
of
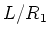
.
Then
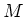
satisfies the following relations.
Since
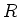
is solvable (and we have assumed
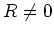
), we see that
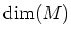
is strictly smaller than
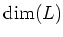
. By induction
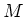
have a Levi subalgebra
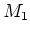
. Then it is clear that
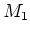
is a
Levi subalgebra of

.
ARRAY(0x9360948)


Next: Abstract Jordan Chevalley decomposition
Up: generalities in finite dimensional
Previous: Semi direct products of
2009-03-06
![]() .
.
![]() and for any
and for any
![]() , we have
, we have
![]() is an
is an ![]() -module which has
-module which has ![]() as
a submodule of codimension
as
a submodule of codimension ![]() .
Thus by using
Lemma 5.51
(Weyl's theorem on irreducibility (codimension
.
Thus by using
Lemma 5.51
(Weyl's theorem on irreducibility (codimension ![]() case)),
we see that there exists a 1-dimensional
case)),
we see that there exists a 1-dimensional ![]() -submodule
-submodule ![]() of
of ![]() (where
(where ![]() is a
is a ![]() submodule of
submodule of ![]() )
such that
)
such that
![]() belongs to
belongs to ![]() , we know the existence of
, we know the existence of ![]() .
The uniqueness of the
.
The uniqueness of the ![]() follows from the assumption that the center of
follows from the assumption that the center of ![]() is trivial.
is trivial.
![]()
![]()