

Next: Bibliography
Up: generalities in finite dimensional
Previous: Levi decomposition
PROOF..
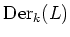
is itself a Lie algebra.
Sending each element
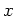
of
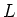
to its ``inner derivation''
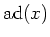
,
we obtain a Lie algebra homomorphism
We note that
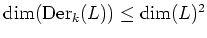
, and that
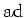
may be
viewed as a homomorphism of
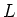
-modules.
(
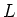
acts on
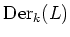
via
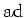
. Namely,
holds for any
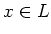
and for any
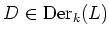
.)
By the Weyl's theorem on complete reducibility,
we see that there exists a
direct sum decomposition
of
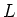
-modules. Then for any
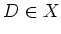
and for any
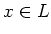
, we see that
So
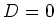
. That means,
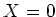
.
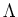
PROPOSITION 5.64
Let 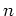 be a positive number
Let
be a positive number
Let 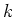 be a separably closed field of characteristic
be a separably closed field of characteristic
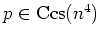 .
We assume further that
.
We assume further that 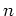 is invertible in
is invertible in 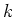 .
(This assumption is provided just in case:
it probably is not necessary because the assumption
.
(This assumption is provided just in case:
it probably is not necessary because the assumption
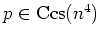 is presumably much stronger.)
Let
is presumably much stronger.)
Let
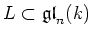 be a linear semisimple Lie algebra.
We assume that the representation
be a linear semisimple Lie algebra.
We assume that the representation
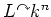 is irreducible.
Then for any element
is irreducible.
Then for any element 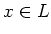 , its semisimple part
, its semisimple part 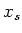 and
its nilpotent part
and
its nilpotent part 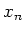 in
in
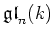 lies in
lies in 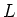 .
.
PROOF..
We may assume
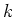
is algebraically closed.
Let
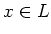
It is enough to prove
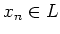
.
There exists a polynomial
![$ f\in k[X]$](img495.png)
such that
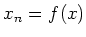
.
Thus we see
Thus
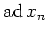
is a derivation of
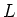
. By the preceding lemma we see that
there exists an element
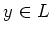
such that
By Schur's lemma, we see that there exists a constant
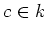
such that
Let us compute traces of both hand sides.
Since
![$ L=[L,L]$](img711.png)
(
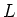
has no non-trivial ideals.), we have
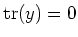
.
Since
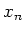
is nilpotent, we have
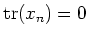
.
Thus we conclude
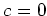
(as we assumed
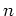
is invertible in
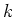
.)
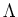
PROOF..
We consider a faithful representation
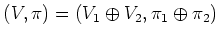
.
For any
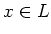
,
satisfies the requirement for the Jordan Chevalley decomposition so by the
uniqueness we see
Now we argue in a same way as in the proof of the previous proposition
and see that there exists a
unique element
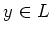
such that
holds. By comparing entries, we obtain
Since
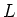
has trivial center, we have
Thus
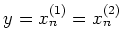
.
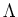
DEFINITION 5.66
Let
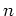
be a positive integer.
Let
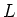
be an
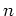
-dimensional semisimple
Lie algebra over a separably closed field
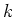
of characteristic
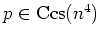
.
Then the
abstract Jordan Chevalley decomposition of
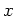
is an decomposition
such that
is the Jordan Chevalley decomposition.
PROOF..
Easy exercise. (Be sure to use Weyl's theorem of complete reducibility.
By taking quotient by a certain ideals (kernels of representations)
one may reduce the proposition to
a case where
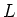
is semisimple and
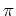
is faithful and irreducible.
)


Next: Bibliography
Up: generalities in finite dimensional
Previous: Levi decomposition
2009-03-06
![]()
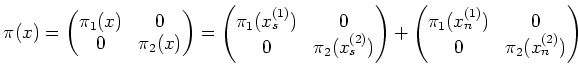
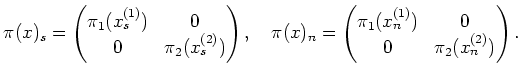
![]()