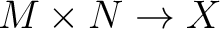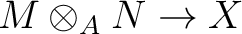Next: additional structures on tensor Up: tensor products and inverse Previous: tensor products of modules
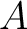 be a (not necessarily commutative) ring.
Let
be a (not necessarily commutative) ring.
Let 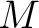 be a right
be a right 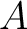 -module. Let
-module. Let  be a left
be a left 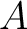 -module.
Then for any module
-module.
Then for any module 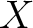 , a map
, a map
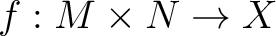 is said to
be an
is said to
be an 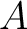 -balanced biadditive map if it
satisfies the following conditions.
-balanced biadditive map if it
satisfies the following conditions.
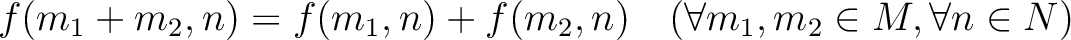
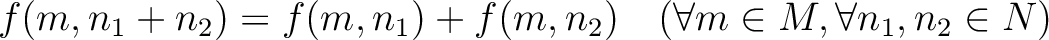
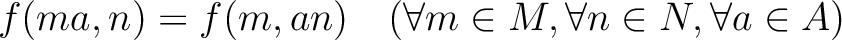
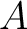 be a (not necessarily commutative) ring.
Let
be a (not necessarily commutative) ring.
Let 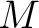 be a right
be a right 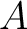 -module. Let
-module. Let  be a left
be a left 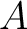 -module.
Then for any module
-module.
Then for any module 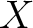 , there is a bijective additive correspondence between
the following two objects.
, there is a bijective additive correspondence between
the following two objects.
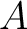 -balanced bilinear map
-balanced bilinear map