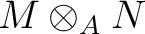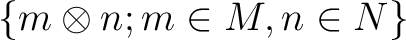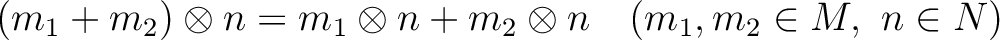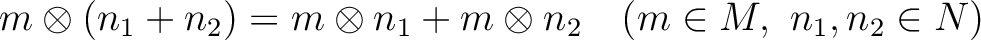Next: universality of tensor products Up: tensor products and inverse Previous: tensor products and inverse
 be a (not necessarily commutative) ring.
Let
be a (not necessarily commutative) ring.
Let  be a right
be a right  -module. Let
-module. Let  be a left
be a left  -module.
Then we define the tensor product of
-module.
Then we define the tensor product of  and
and  over
over  , denoted by
, denoted by