三種類の無限小変形
![]() を
を ![]() 上の可換スキームとする。
上の可換スキームとする。![]() の一次の無限小変形を考えよう。
の一次の無限小変形を考えよう。
![]() を
を
![]() 上の非可換スキームに延長しようと言うわけである。
これには要は
上の非可換スキームに延長しようと言うわけである。
これには要は ![]() 上の加群の層
上の加群の層
![]() に
に
![]() -双線型な
乗法
-双線型な
乗法
![]() を
を
さて、
![]() が結合律を満たすための条件を書き下してみると、
が結合律を満たすための条件を書き下してみると、
![]() があるコサイクル条件を満たすべし、と言うかたちに落ち着く
のがわかる。このコサイクルを然るべき同値類で類別したものは
ホッホシルトコホモロジーの言葉で
があるコサイクル条件を満たすべし、と言うかたちに落ち着く
のがわかる。このコサイクルを然るべき同値類で類別したものは
ホッホシルトコホモロジーの言葉で
![]() と書かれるものである。
あるいは別の言葉で言えば上のことは
と書かれるものである。
あるいは別の言葉で言えば上のことは
![]() の
の
![]() による拡大を考えている
ことに当たるので、
による拡大を考えている
ことに当たるので、
![]() の変わりに
の変わりに
![]() (
(
![]() )
と書いても良い。両者は同じものである。
)
と書いても良い。両者は同じものである。
この
![]() をもう少し見慣れたもので表現することを
考えてみよう。導来函手の間の等式
をもう少し見慣れたもので表現することを
考えてみよう。導来函手の間の等式
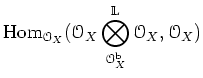
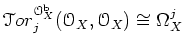
正確な条件は何だったか忘れたが、
![]() が良いものの場合には上のスペクトル系列(5.1)
は退化する。したがって、一次の無限小変形をパラメトライズする空間は
が良いものの場合には上のスペクトル系列(5.1)
は退化する。したがって、一次の無限小変形をパラメトライズする空間は
以下の議論での引用のためにここで二次元射影非可換スキームに関する 次の予想を載せておく。
Conjecture of M. Artin ([2])
Let ![]() be an algebraically closed field of characterstic zero, and
let
be an algebraically closed field of characterstic zero, and
let ![]() be
be ![]() -algebra of dimension 3 sastisfying the ``good'' properties.
Then
one of the following holds:
-algebra of dimension 3 sastisfying the ``good'' properties.
Then
one of the following holds:
容易に想像がつくように、q-rational, q-ruled な非可換スキームとは それぞれ rational, ruled な(通常の)曲面の変形に当たる。 上の予想は、それ以外は可換スキームに毛を生やしたようなもの (可換スキーム上の代数の層)しかないと主張している。