

Next: 螺旋階段を上から覗いてみる
Up: Vista:リーマン面
Previous: この節のまとめ
前節の前置きが長くなりましたが、この節でいよいよ指数関数のグラフを描いてみましょう。
mupad を使うことによって、3次元のグラフはたやすく描くことが出来るから、
あとは一次元分をどのように落とすかです。
指数関数
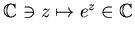 のグラフとは、
のグラフとは、
を全ての複素数 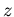 についてプロットしたものですから、
実関数で全て実の世界に戻すと、
についてプロットしたものですから、
実関数で全て実の世界に戻すと、
を全ての実数の組 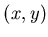 について4次元にプロットすればよろしい。
について4次元にプロットすればよろしい。
ここで、(☆)の一番先頭の 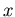 を落としてしまうことにすれば、めでたく3次元のグラフが描けます。
実際、
を落としてしまうことにすれば、めでたく3次元のグラフが描けます。
実際、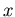 は他の成分から逆算可能だから、落としてもあとから
頭の中で復活できるのです。
は他の成分から逆算可能だから、落としてもあとから
頭の中で復活できるのです。
このグラフをを書くためのmupad のプログラム

Yoshifumi Tsuchimoto
2000-04-12
![]() のグラフとは、
のグラフとは、
![]() を落としてしまうことにすれば、めでたく3次元のグラフが描けます。
実際、
を落としてしまうことにすれば、めでたく3次元のグラフが描けます。
実際、![]() は他の成分から逆算可能だから、落としてもあとから
頭の中で復活できるのです。
は他の成分から逆算可能だから、落としてもあとから
頭の中で復活できるのです。
