

Next: Vista:リーマン面
Up: 対数関数の多価性について
Previous: 偏角を選ぶことの面倒な点
等式
の右辺で、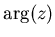 のとり方を制限することにより、
一価な関数
のとり方を制限することにより、
一価な関数
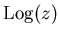 を得ることは出来る。
しかしこの関数は他の重要な性質を完全には満たしておらず、
いつでも満足できると言うわけにはいかない。
もっと短く言うと、
を得ることは出来る。
しかしこの関数は他の重要な性質を完全には満たしておらず、
いつでも満足できると言うわけにはいかない。
もっと短く言うと、
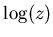 を
を 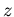 の一価関数として定義したい。
の一価関数として定義したい。
という欲求と、
が(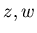 の範囲に制限をつけたり
の範囲に制限をつけたり 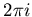 の整数倍を度外視するといった
ことをせずに無条件に)成り立って欲しいという欲求は相反する面を持っており、
同時に成り立たせるのは(このままでは)不可能である。
の整数倍を度外視するといった
ことをせずに無条件に)成り立って欲しいという欲求は相反する面を持っており、
同時に成り立たせるのは(このままでは)不可能である。
Yoshifumi Tsuchimoto
2000-04-12
![]() を
を ![]() の一価関数として定義したい。
の一価関数として定義したい。