三角関数の巾級数表示

前章では指数関数が巾級数表示を持つことについて述べたが、 じつは三角関数も同様な表示を持つことが知られている。 答えだけここに記しておくことにする。

$$\cos(z)=\sum_{k=0}^\infty (-1)^k\frac{1}{(2k)!}z^{2k}$$

$$\sin(z)=\sum_{k=0}^\infty (-1)^k\frac{1}{(2k-1)!}z^{2k-1}$$

これらの巾級数も、指数関数の場合とように、収束が速く、取り扱いやすい。

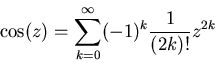
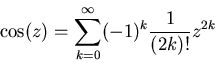
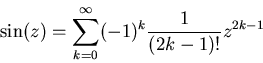
指数関数、三角関数をはじめとするいろいろな関数が巾級数で書けるのは 驚くべきことのような気がする。 このことを発見した人々はワクワクしただろうことは、想像に難くない。

関数を巾級数で書く利点の一つは、 前章ですでに見たように、それを容易に複素数の関数と見倣せるという点にある。 三角関数も、上に挙げた巾級数表示により、複素数の関数と見倣せるのである。 これは、三角関数の幾何学的な定義のみを眺めていたのでは、気がつきにくい 点だろう。

円弧の長さと言うような幾何学的な関数を複素数に拡張して、意味があるのだろうか、 と思われる方々もいられると思うが、実はそれが大ありなのだ。 じゃあ「円」じゃなくて「楕円」ならどうか？それはこの項の主題から 少し外れるが、実に面白い話題である。興味のある人は高木貞二著 「近世数学史談」および「雑談」などをさんしょうされるとよい。