![]() の平方根というのが前節で出て来たけが、これは本当に新しい数なのだろうか?
「新しい数」を導入するのももちろん面白い考え方だけれども、
まず今までの複素数で本当に
の平方根というのが前節で出て来たけが、これは本当に新しい数なのだろうか?
「新しい数」を導入するのももちろん面白い考え方だけれども、
まず今までの複素数で本当に ![]() の平方根がないのかどうか
確かめるのもとても大事だ。試しに
の平方根がないのかどうか
確かめるのもとても大事だ。試しに

(「新しい数を導入する基準は何なんだ、」あるいは、
「本当に ![]() なんて導入して良かったんだろうか?」という疑問が出そうだ。
既存の「数」に新しい「数」を付け加えてどうなるかを調べることは、例えば
代数学でよく取り扱われることで、
「環や体の拡大の理論」と呼ばれるものがそれにあたる。
拡大(新しい数を付け加えること)ができたとして、
それがとても良い性質を満たすかどうかは、解析学などでも重要なテーマで、
たとえば複素数にたいしては「複素解析学」と呼ばれる美しい理論があって、
複素数導入の動機付けの一つを与えている。)
なんて導入して良かったんだろうか?」という疑問が出そうだ。
既存の「数」に新しい「数」を付け加えてどうなるかを調べることは、例えば
代数学でよく取り扱われることで、
「環や体の拡大の理論」と呼ばれるものがそれにあたる。
拡大(新しい数を付け加えること)ができたとして、
それがとても良い性質を満たすかどうかは、解析学などでも重要なテーマで、
たとえば複素数にたいしては「複素解析学」と呼ばれる美しい理論があって、
複素数導入の動機付けの一つを与えている。)
じつは、もう一つ別のやり方で![]() の平方根を出すこともできる。
の平方根を出すこともできる。
もう一つ計算してみよう。3乗して ![]() になる複素数はどれぐらいあるか
ご存知だろうか?
になる複素数はどれぐらいあるか
ご存知だろうか?
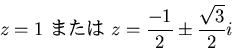
これらの、《何とか乗して ![]() になる数》のことをよく「一の巾根」
とよぶ。(そのまんまやんけ!)
になる数》のことをよく「一の巾根」
とよぶ。(そのまんまやんけ!)
一の巾根をガウス平面にプロットしてみると、実に面白いことに気づく。
これは「複素数の積が幾何学的にはどのように解釈できるか」という ことから説明できる。面白いから是非試してみてほしい。
上の最後の主張は、いままで関係ないと思っていた三角関数が、
実は巾乗を考える上で大事なことを意味している。
次の節でその点に少し触れよう。