
Next: 複素数について
Up: 解説編
Previous: この節のまとめ
前節の「巾級数表示」を使うと、複素数 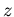 に対して、
に対して、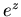 を定義すること
ができる。
実際、
を定義すること
ができる。
実際、
の右辺を眺めてみると、これを計算するには足し算、引き算、かけ算、および
極限操作ができれば良いことがわかる。
このうち、複素数を習ったことのある人にとって明解でないのは
極限操作(無限和の部分の収束性)だけだろう。
複素数の極限操作は、実は「複素数の絶対値」を物差しに使うことにより
実数と同様な取り扱いをすることができる。
詳しくは複素解析学の教科書の最初のほうを開いてみて頂きたい。
Yoshifumi Tsuchimoto
2000-04-12