Next: sheafication of a sheaf Up: , , and the Previous: homomorphisms of (pre)sheaves
 on an affine schemes are “too good”. Namely,
in terms of cohomology (which we study later,) we have always
on an affine schemes are “too good”. Namely,
in terms of cohomology (which we study later,) we have always
 if
if 
So to study some important problems on sheaf theory (which we will sure to encounter when we deal with non-affine schemes,) we need to study some examples from other mathematical areas.
A first example is a presheaf which satisfies the “locality” of sheaf axiom, but which fails to obey “gluing lemma”.
 be the (usual) real line with the usual Lebesgue measure.
Then we have a presheaf of
be the (usual) real line with the usual Lebesgue measure.
Then we have a presheaf of  -functions given by
-functions given by
 is integrable
is integrable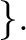
 is a presheaf which satisfies the “locality” of sheaf axiom,
but which fails to obey “gluing lemma”.
Indeed, Let
is a presheaf which satisfies the “locality” of sheaf axiom,
but which fails to obey “gluing lemma”.
Indeed, Let
 be an open covering of
be an open covering of
 and define
a section
and define
a section  on
on  by
by

 is a family of sections which satisfies
the assumption of “gluing lemma”. The function which should
appear as the “glued function” is the constant function
is a family of sections which satisfies
the assumption of “gluing lemma”. The function which should
appear as the “glued function” is the constant function  , which
fails to be integrable on the whole of
, which
fails to be integrable on the whole of
 .
.
We may “sheaficate” the presheaf  above.
Instead of
above.
Instead of  -functions we consider functions which are locally
-functions we consider functions which are locally  .
Namely, for any open subset
.
Namely, for any open subset
 , we consider
, we consider

 -functions”.
-functions”.
 Bdd
Bdd of bounded functions on a topological
space
of bounded functions on a topological
space 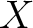 . We may sheaficate this example and the sheaf so created is
the sheaf of locally bounded functions.
. We may sheaficate this example and the sheaf so created is
the sheaf of locally bounded functions.
For any differentiable ( ) manifold
) manifold 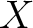 (students
which are not familiar with the manifolds may take
(students
which are not familiar with the manifolds may take 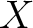 as an open
subset of
as an open
subset of
 for an example.),
we define a presheaf
for an example.),
we define a presheaf
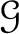 on
on 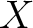 defined as follows
defined as follows
 complex valued $C^&infin#infty;$-functions on $U×U$
complex valued $C^&infin#infty;$-functions on $U×U$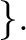
To sheaficate this, we first need to introduce an equivalence relation on
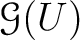 .
.
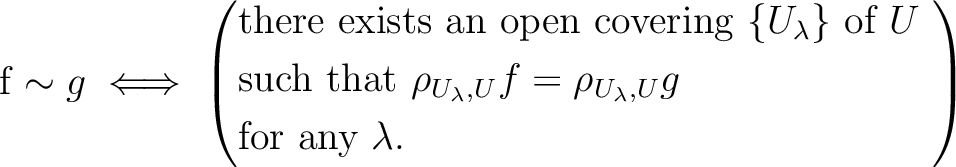

Then we define

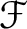 so defined
is a sheaf.
(Readers who are familiar with the theory of jets may notice that
the sheaf is related to the sheaf of jets. In other words, there is a
sheaf homomorphism from this sheaf to the sheaf of jets.)
so defined
is a sheaf.
(Readers who are familiar with the theory of jets may notice that
the sheaf is related to the sheaf of jets. In other words, there is a
sheaf homomorphism from this sheaf to the sheaf of jets.)