Next: example of presheaves and Up: , , and the Previous: Benefit of being a
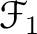 ,
,
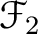 be presheaves of modules on a topological space
be presheaves of modules on a topological space 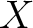 .
Then we say that a sheaf homomorphism
.
Then we say that a sheaf homomorphism
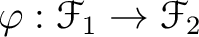
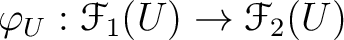
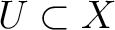 with the following property hold.
with the following property hold.
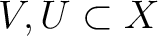 such that
such that
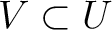 , we have
, we have
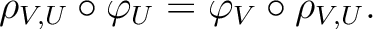
 commutes with restrictions”.)
commutes with restrictions”.)