- a set
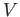 , whose elements are called vertices or nodes,
, whose elements are called vertices or nodes,
- a set
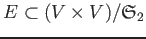 of unordered pairs of vertices, called edges.
of unordered pairs of vertices, called edges.
Let ![]() be a graph.
The Ihara zeta function of
be a graph.
The Ihara zeta function of ![]() is defined by
is defined by
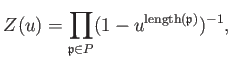
where
We define the adjacency operator ![]() as
as
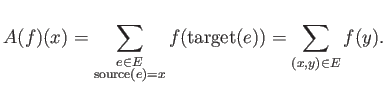
We also define the `degree operator' ![]() as:
as:
where the degree
where