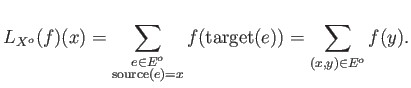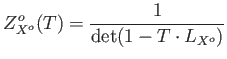- a set
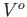 , whose elements are called vertices or nodes,
, whose elements are called vertices or nodes,
- a set
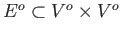 of ordered pairs of vertices, called directed edges.
of ordered pairs of vertices, called directed edges.
Let
![]() be a directed graph.
For each positive integer
be a directed graph.
For each positive integer ![]() , we let
, we let ![]() to be the number of
admissible closed paths in
to be the number of
admissible closed paths in ![]() .
Then we put
.
Then we put
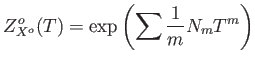
We define Perron Frobeinus operator
![]() to be
to be