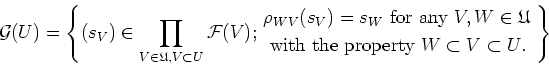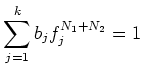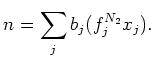PROOF..
We prove (2).
From the previous Lemma, we only need to prove locality and gluing lemma for
open sets of the form  . That means, in proving the properties
(1) and (2) of Definition 1.19, we may assume that
. That means, in proving the properties
(1) and (2) of Definition 1.19, we may assume that
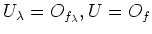 for some elements
for some elements
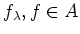 .
.
Furthermore, in doing so we may use the identification
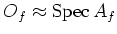 .
By replacing
.
By replacing 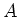 by
by 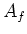 , this means that we may assume that
, this means that we may assume that
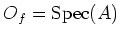 .
.
To sum up, we may assume
To simplify the notation, in the rest of the proof, we shall denote by
the canonical map which we have formerly written
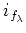
.
Furthermore, for any pair
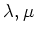
of the index set,
we shall denote by
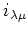
the canonical map
Locality:
Compactness of
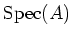
(Theorem
1.12) implies that
there exist finitely many open sets
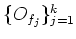
among
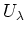
such that
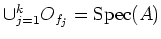
.
In particular there exit elements
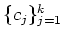
of
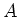
such that
|
(PU) |
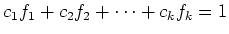 |
holds.
Let 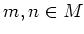 be elements such that
be elements such that
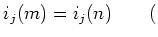
in
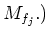
With the help of the ``module version'' of Lemma
1.8,
we see that for each
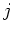
, there exist positive integers
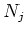
such that
holds for all
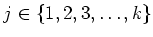
.
Let us take the maximum
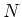
of
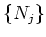
. It is easy to see that
holds for any
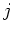
. On the other hand, taking
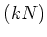
-th power of the equation
(PU) above, we may find elements
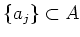
such that
holds.
Then we compute
to conclude that
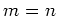
.
Gluing lemma:
Let
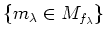 be given
such that they satisfy
be given
such that they satisfy
for any
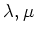
.
We fist choose a finite subcovering
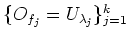
of
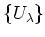
.
Then we may choose a positive integer
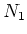
such that
holds for all
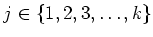
.
Then by the same argument which appears in the ``locality" part,
there exists a positive integer
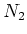
such that
holds for all
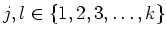
.
We rewrite the above equation as follows.
On the other hand, by taking
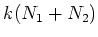
-th power of the equation (PU),
we may see that there exist elements
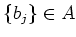
such that
holds.
Now we put
Then since for any 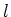
holds on
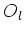
, we have
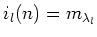
.
Now, take any other open set
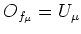 from the covering
from the covering
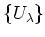 .
.
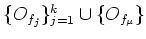 is again a finite open
covering of
is again a finite open
covering of
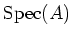 .
We thus know from the argument above that there exists an element
.
We thus know from the argument above that there exists an element 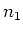 of
of
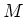 such that
such that
From the locality,
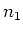
coincides with
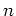
.
In particular,
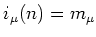
holds.
This means
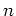
satisfies the requirement for the ``glued object''.
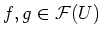 such that
such that
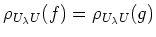
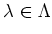 , then we have
, then we have 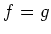
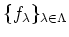 such that
such that
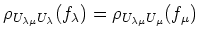
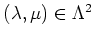 , then we have
a section
, then we have
a section
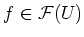 such that
such that
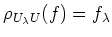
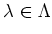 .
.