


: ïŋ―ïŋ―ïŋ―ïŋ―Ęļïŋ―ïŋ―ËĪÄĪïŋ―ïŋ―ïŋ―...
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―II ïŋ―ïŋ―ïŋ―ïŋ― No.11
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĨÆĄïŋ―ïŋ―ïŋ―:

ïŋ―ïŋ―ïŋ―ïŋ― 11.1
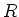
ïŋ―ÏīÄĪĮĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Įŋïŋ―
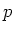
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÃĪÆĄïŋ―
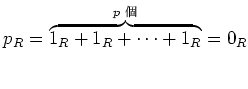
ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ÎĐïŋ―ÃĪÆĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ÎĪČĪïŋ―ïŋ―ïŋ―
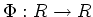
ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÐĄïŋ―
ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―éĪ―ïŋ―ėžŦïŋ―ČĪØĪÎ―ïŋ―Æąïŋ―ïŋ―(ïŋ―ïŋ―ïŋ―Ę―ïŋ―Æąïŋ―ïŋ―)ïŋ―ïŋ―Íŋïŋ―ïŋ―ïŋ―ëĄĢ
 ïŋ―ïŋ―
ïŋ―ïŋ― 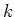 ïŋ―ó·ŦĪïŋ―ïŋ―ÖĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ó·ŦĪïŋ―ïŋ―ÖĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ― 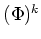 ïŋ―ïŋ―
ïŋ―ïŋ―Íŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĪģïŋ―ČĪËĪïŋ―ïŋ―ïŋ―ïŋ―ÕĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―
ïŋ―ïŋ―Íŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĪģïŋ―ČĪËĪïŋ―ïŋ―ïŋ―ïŋ―ÕĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ― 11.1
ïŋ―Įŋïŋ―
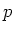
ïŋ―ÎĨŲĨïŋ―
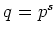
ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĄïŋ―
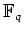
ïŋ―Îģïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
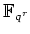
ïŋ―Ξïŋ―ïŋ―ïŋ―Æąïŋ―ïŋ―
ïŋ―ïŋ―
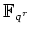
ïŋ―ïŋ―
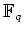
ïŋ―ïŋ―ÎĨÕĨïŋ―ïŋ―ŲĨËĨïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Æąïŋ―ïŋ―ïŋ―ČļÆĪÖĄïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 11.3
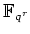
ïŋ―ïŋ―
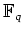
ïŋ―ïŋ―Ξïŋ―ïŋ―ïŋ―Æąïŋ―ïŋ―
(
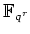
ïŋ―ïŋ―ïŋ―ïŋ―
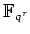
ïŋ―ØĪΞïŋ―ïŋ―ïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
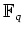
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÂĪïŋ―ïŋ―ïŋ―Čđïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĪĘĪïŋ―ïŋ―ïŋ―)ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪÏĄïŋ―
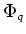
ïŋ―ËĪïŋ―ÃĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ėŋïŋ―
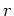
ïŋ―Î―ïŋ―ó·ēĪĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―11.2ïŋ―ïŋ―(1)ïŋ―Îģïŋ―ÄĨïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ― 11.4
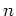
ïŋ―Ņŋïŋ―ïŋ―ïŋ―Âŋïŋ―āž°
![% latex2html id marker 1240
$ f_1,f_2,\dots,f_m \in {\mathbb{F}}_q[X_1,X_2,\dots,X_n]$](img30.png)
ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
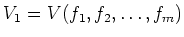
ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĄïŋ―
ïŋ―ÖĨÕĨïŋ―ïŋ―ŲĨËĨïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
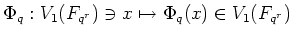
ïŋ―ōžĄĪÎĪčĪĶïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
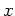
ïŋ―ïŋ―
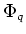
ïŋ―ïŋ―ïŋ―ïŋ―Æ°ïŋ―ïŋ― (
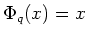
)ïŋ―ĮĪïŋ―ïŋ―ëĪģïŋ―ČĪČĄïŋ―
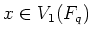
ïŋ―ĮĪïŋ―ïŋ―ëĪģïŋ―ČĪČĪïŋ―Æąïŋ―ÍĪĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ÜđÖĩïŋ―ïŋ―ĮĪÏŋïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ïđïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Øŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Äīïŋ―ŲĪïŋ―Į―ïŋ―ÎĨŌĨïŋ―ČĪËĪĘĪëĄĢ
1ïŋ―Ņŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĨïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Øŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ęĪ·ïŋ―ÆĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ÞĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĪÄĪïŋ―ïŋ―ÆĪÎīïŋ―Ãąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ęĪŦïŋ―ïŋ―
Ėŋïŋ―ïŋ― 11.1
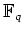
ïŋ―ïŋ―Îīïŋ―ïŋ―ïŋ―ïŋ―1ïŋ―Ņŋïŋ―Âŋïŋ―āž°
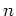
ïŋ―ïŋ―Âŋïŋ―āž°
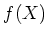
ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĄïŋ―
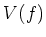
ïŋ―Îđïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Øŋïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―Íŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÃĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĄïŋ―ïŋ―ïŋ―ïŋ―ÎĢïŋ―ïŋ―ïŋ―ÏĪïŋ―ïŋ―ĘĪïŋ―ōĪĪäĪđïŋ―ïŋ―ïŋ―ĘĪëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ― 8.1 ïŋ―ïŋ―ïŋ―ÎĪčĪĶïŋ―ïŋ―(1)-(3)ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―((4)ïŋ―ïŋ―ïŋ―ōĪĪäĪđïŋ―ïŋ―ïŋ―čĪĶïŋ―ïŋ―)ïŋ―ïŋ―ïŋ―,(4)ïŋ―ïŋ― ïŋ―ïŋ―
ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
(1) ïŋ―Įŋïŋ― 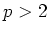
(2) ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ― 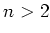
(3)
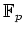 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÛĪĘĪïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÛĪĘĪïŋ― 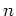 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Âŋïŋ―āž°
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Âŋïŋ―āž°
![$ f,g\in{\mathbb{F}}_p[X]$](img54.png)
(4)
![$ {\mathbb{F}}_p[X]/f(X){\mathbb{F}}_p[X]$](img55.png) ïŋ―ĮĪïŋ―
ïŋ―ĮĪïŋ― 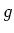 ïŋ―ΰėžĄïŋ―ïŋ―ïŋ―ØĪïŋ―
ĘŽïŋ―ïŋ―
ïŋ―ΰėžĄïŋ―ïŋ―ïŋ―ØĪïŋ―
ĘŽïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 9.1 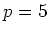 ïŋ―ČĪïŋ―ïŋ―ëĄĢ
ïŋ―ČĪïŋ―ïŋ―ëĄĢ
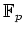 ïŋ―ïŋ―ÎĨïŋ―ËĨÃĨïŋ―ïŋ―ïŋ―4ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Âŋïŋ―ïŋ―
ïŋ―ïŋ―
ïŋ―ïŋ―ÎĨïŋ―ËĨÃĨïŋ―ïŋ―ïŋ―4ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Âŋïŋ―ïŋ―
ïŋ―ïŋ― 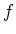 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―óĪēĄïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―óĪēĄïŋ― 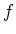 ïŋ―ΰïŋ―ÄĪΚïŋ―ïŋ―ïŋ―
ïŋ―ΰïŋ―ÄĪΚïŋ―ïŋ―ïŋ― 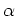 ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ― 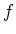 ïŋ―ïŋ―Âū
ïŋ―Κïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―Âū
ïŋ―Κïŋ―ïŋ―ïŋ― 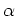 ïŋ―ĮĪïŋ―ïŋ―ïŋ―ïĪ·ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ― (ïŋ―ÄĪÞĪęĄĒ
ïŋ―ĮĪïŋ―ïŋ―ïŋ―ïĪ·ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ― (ïŋ―ÄĪÞĪęĄĒ 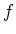 ïŋ―ïŋ―
ïŋ―ïŋ―
![$ {\mathbb{F}}_p[\alpha]$](img58.png) ïŋ―ïŋ―Į°ėžĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ŅĪïŋ―ĘŽïŋ―ōĪ·ĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―)
ïŋ―ïŋ―Į°ėžĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ŅĪïŋ―ĘŽïŋ―ōĪ·ĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―)
ïŋ―ïŋ―ïŋ―ïŋ― 11.1
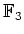
ïŋ―ïŋ―ïŋ―Âŋïŋ―āž°
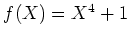
ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĄïŋ―
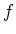 ïŋ―ïŋ―
ïŋ―ïŋ―
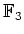 ïŋ―ïŋ―Îīïŋ―ïŋ―ïŋ―ïŋ―Âŋïŋ―āž°ïŋ―ïŋ―ïŋ―ŅĪïŋ―ĘŽïŋ―ōĪ·ĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―Îīïŋ―ïŋ―ïŋ―ïŋ―Âŋïŋ―āž°ïŋ―ïŋ―ïŋ―ŅĪïŋ―ĘŽïŋ―ōĪ·ĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
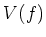 ïŋ―Îđïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Øŋïŋ―
ïŋ―Îđïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Øŋïŋ― 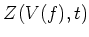 ïŋ―ïŋ―ïŋ―ïŋ―čĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―čĄĢ
(ïŋ―ŌĨïŋ―ïŋ―:
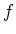
ïŋ―ïŋ―
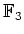
ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ĮĪÏĪĘĪïŋ―ïŋ―ÎĪĮĄïŋ―Ėŋïŋ―ïŋ―
11.1ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ÎĪÞĪÞĪĮĪÏŧČĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―)
ïŋ―ïŋ―ïŋ―ïŋ― 11.2
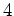
ïŋ―Įģïŋ―ïŋ―ïŋ―
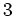
Íūïŋ―ïŋ―čĪĶïŋ―ïŋ―ïŋ―Įŋïŋ―
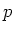
ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĪÏĄïŋ―
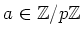
ïŋ―ïŋ―
ïŋ―ÉĪÎĪčĪĶïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪâĄĒ
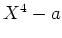
ïŋ―ïŋ―
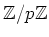
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĪĘĪïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ČĪōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
(ïŋ―ŌĨïŋ―ïŋ―:ĮĪïŋ―ÕĪïŋ―ïŋ―Įŋïŋ― 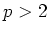 ïŋ―ïŋ―
ïŋ―ïŋ―
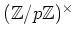 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ― 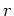 ïŋ―ČĪïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĄïŋ―
ïŋ―ČĪïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĄïŋ―
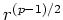 ïŋ―ïŋ―
ïŋ―ïŋ―
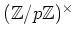 ïŋ―ΰĖŋïŋ―
ïŋ―ΰĖŋïŋ― 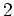 ïŋ―Îļïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ(ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―))
ïŋ―Îļïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ(ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―))
ïŋ―ïŋ―ïŋ―ïŋ― 11.4
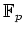
ïŋ―Îļïŋ―
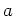
ïŋ―ĮĄïŋ―ïŋ―ÉĪïŋ―ïŋ―
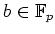
ïŋ―ïŋ―ČĪÃĪÆĪïŋ―ïŋ―ÆĪïŋ―
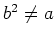
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―Íŋïŋ―ïŋ―ïŋ―ïŋ―ėĪŋïŋ―ČĪïŋ―ïŋ―ëĄĢ
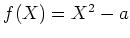
ïŋ―ČĪïŋ―ïŋ―ïŋ―
![$ R={\mathbb{F}}_p[X]/f(X){\mathbb{F}}_p[X]$](img77.png)
ïŋ―ïŋ―
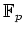
ïŋ―ïŋ―ïŋ―
2ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ŲĨïŋ―ïŋ―ČĨïŋ―ïŋ―ïŋ―ÖĪČļïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―
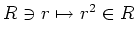
ïŋ―ïŋ―É―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―čĪĶïŋ―ïŋ―
2ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
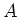
ïŋ―ïŋ―ïŋ―ČĪáĄĒ
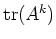
ïŋ―ïŋ―Ũŧïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
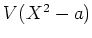
ïŋ―Îđïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Øŋïŋ―ïŋ―ČĪïŋ―ïŋ―ηïŋ―ĖĪÎīØ·ïŋ―ïŋ―ËĪÄĪïŋ―ïŋ―ÆĄïŋ―ïŋ―ïĪŦïŋ―ëĪģïŋ―ČĪïŋ―
(ïŋ―ŨĪïŋ―ïŋ―ÕĪïŋ―ïŋ―ÂĪïŋ―)ïŋ―ŌĪŲĪčĄĢ
(
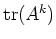 ïŋ―ïŋ―
ïŋ―ïŋ―
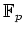 ïŋ―Îļïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĪŦïŋ―éĄĒïŋ―ÖļÄŋïŋ―ïŋ―ŨĪČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―(
ïŋ―Îļïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĪŦïŋ―éĄĒïŋ―ÖļÄŋïŋ―ïŋ―ŨĪČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―(
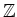 ïŋ―Îļïŋ―)
ïŋ―ïŋ―ïŋ―ïŋ―ŲĪïŋ―Čūïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĖĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĄïŋ―
ïŋ―Îļïŋ―)
ïŋ―ïŋ―ïŋ―ïŋ―ŲĪïŋ―Čūïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĖĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĄïŋ―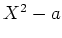 ïŋ―ïŋ―ĮĪïŋ―ÕĪÎīïŋ―ïŋ―ïŋ―Âŋïŋ―āž°ïŋ―ïŋ―ïŋ―ÖĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―Æąïŋ―ÍĪÎĪïŋ―ïŋ―ČĪïŋ―
ïŋ―ĮĪïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ïūïŋ―ïŋ―ïŋ―ïŋ―ņĪ·Īïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪĮĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ÆĪÏēÝĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―)
ïŋ―ïŋ―ĮĪïŋ―ÕĪÎīïŋ―ïŋ―ïŋ―Âŋïŋ―āž°ïŋ―ïŋ―ïŋ―ÖĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―Æąïŋ―ÍĪÎĪïŋ―ïŋ―ČĪïŋ―
ïŋ―ĮĪïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ïūïŋ―ïŋ―ïŋ―ïŋ―ņĪ·Īïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪĮĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ÆĪÏēÝĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―)



: ïŋ―ïŋ―ïŋ―ïŋ―Ęļïŋ―ïŋ―ËĪÄĪïŋ―ïŋ―ïŋ―...
2002ĮŊ7ïŋ―ïŋ―2ïŋ―ïŋ―
![]()
 ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ÎĐïŋ―ÃĪÆĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ÎĪČĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ÎĐïŋ―ÃĪÆĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ÎĪČĪïŋ―ïŋ―ïŋ―
![]()
![]()
![]() ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÛĪĘĪïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÛĪĘĪïŋ― ![]() ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Âŋïŋ―āž°
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Âŋïŋ―āž°
![]()
![]() ïŋ―ĮĪïŋ―
ïŋ―ĮĪïŋ― ![]() ïŋ―ΰėžĄïŋ―ïŋ―ïŋ―ØĪïŋ―
ĘŽïŋ―ïŋ―
ïŋ―ΰėžĄïŋ―ïŋ―ïŋ―ØĪïŋ―
ĘŽïŋ―ïŋ―
![]() ïŋ―ČĪïŋ―ïŋ―ëĄĢ
ïŋ―ČĪïŋ―ïŋ―ëĄĢ
![]() ïŋ―ïŋ―ÎĨïŋ―ËĨÃĨïŋ―ïŋ―ïŋ―4ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Âŋïŋ―ïŋ―
ïŋ―ïŋ―
ïŋ―ïŋ―ÎĨïŋ―ËĨÃĨïŋ―ïŋ―ïŋ―4ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Âŋïŋ―ïŋ―
ïŋ―ïŋ― ![]() ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―óĪēĄïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―óĪēĄïŋ― ![]() ïŋ―ΰïŋ―ÄĪΚïŋ―ïŋ―ïŋ―
ïŋ―ΰïŋ―ÄĪΚïŋ―ïŋ―ïŋ― ![]() ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ― ![]() ïŋ―ïŋ―Âū
ïŋ―Κïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―Âū
ïŋ―Κïŋ―ïŋ―ïŋ― ![]() ïŋ―ĮĪïŋ―ïŋ―ïŋ―ïĪ·ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ― (ïŋ―ÄĪÞĪęĄĒ
ïŋ―ĮĪïŋ―ïŋ―ïŋ―ïĪ·ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ― (ïŋ―ÄĪÞĪęĄĒ ![]() ïŋ―ïŋ―
ïŋ―ïŋ―
![]() ïŋ―ïŋ―Į°ėžĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ŅĪïŋ―ĘŽïŋ―ōĪ·ĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―)
ïŋ―ïŋ―Į°ėžĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ŅĪïŋ―ĘŽïŋ―ōĪ·ĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―)