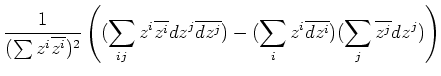

: 余談:Fubini-Study 計量の形式的な導き方について
: 複素射影空間
: 複素射影空間のケーラー構造
この節では、Fubini-Study 計量の幾何学的な定義について
振り返ってみよう。
次のように、
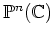 は
は 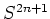 の商空間と見倣せる。
の商空間と見倣せる。
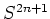 には
には
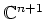 から誘導された計量が入り、
それは
から誘導された計量が入り、
それは 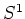 の作用で不変だから、
の作用で不変だから、
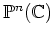 の計量を定める。
これが
の計量を定める。
これが
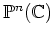 の Fubini-Study 計量である。
の Fubini-Study 計量である。
本稿では余り用いないが、Fubini-Study 計量の座標表示についても
一応触れておこう。
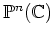 の複素斉次座標
の複素斉次座標
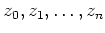 をとる。
をとる。
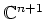 の各点の接ベクトルを
の各点の接ベクトルを
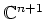 の元と同一視しておく。
の元と同一視しておく。
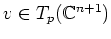 の長さは、
の長さは、
であたえられる。
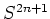 の計量を求めよう。
の計量を求めよう。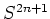 の点
の点 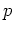 における
における
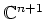 の接ベクトル
の接ベクトル 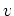 を考える。
を考える。
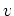 を
を 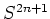 に関する接平面の成分と法線方向の成分に分解し、
接平面成分の長さを求めることが必要になる。
に関する接平面の成分と法線方向の成分に分解し、
接平面成分の長さを求めることが必要になる。
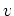 と
と 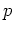 とのなす角を
とのなす角を 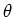 とおくと、内積に関する有名な公式
とおくと、内積に関する有名な公式
今の場合 $||p||=1$ だから
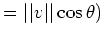
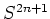 の計量になる。
の計量になる。
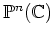 の計量を得るためには、
ここからさらに
の計量を得るためには、
ここからさらに 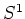 -作用の方向の成分を引き去る必要がある。
上と同様の考え方によって、
-作用の方向の成分を引き去る必要がある。
上と同様の考え方によって、
($v$ の、$S^n+1$ に接し、$S^1$ 軌道 と垂直な成分の長さ)
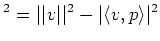
座標を使って表現すると、Fubini-Study 計量を与える(もととなる) 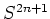 上の計量は、
上の計量は、
と言うことになる。
話を
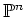 らしくするために、
らしくするために、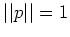 への制限を
やめて、長さ
への制限を
やめて、長さ 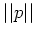 に関して斉次な形で書くと、次のようになる。
に関して斉次な形で書くと、次のようになる。
これが斉次座標で表現した Fubini-Study 計量であって、
非斉次座標に移るには定石通り一つの 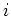 に関して
に関して
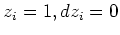 とおいてやれば良い。
詳細は読者にお任せしよう。
とおいてやれば良い。
詳細は読者にお任せしよう。
平成16年8月24日
![]() は
は ![]() の商空間と見倣せる。
の商空間と見倣せる。
![]() の複素斉次座標
の複素斉次座標
![]() をとる。
をとる。
![]() の各点の接ベクトルを
の各点の接ベクトルを
![]() の元と同一視しておく。
の元と同一視しておく。
![]() の長さは、
の長さは、
![]() と
と ![]() とのなす角を
とのなす角を ![]() とおくと、内積に関する有名な公式
とおくと、内積に関する有名な公式
![]() 上の計量は、
上の計量は、
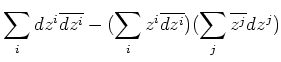
![]() らしくするために、
らしくするために、![]() への制限を
やめて、長さ
への制限を
やめて、長さ ![]() に関して斉次な形で書くと、次のようになる。
に関して斉次な形で書くと、次のようになる。