

: 複素射影空間
: 最初の例:コタンジェントバンドル
: コタンジェントバンドルのシンプレクティック構造
微分作用素の環は(微分作用素としての)階数によってフィルターづけされる。
このフィルターづけされた環の"Gr" をとったのが 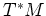 の上の関数環
である。
の上の関数環
である。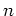 階の微分作用素
階の微分作用素
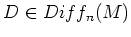 が代表する
が代表する
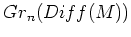 の元を
の元を 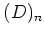 と書くことにする。
と書くことにする。
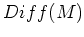 のフィルトレーションは次のような特徴をもつ。
のフィルトレーションは次のような特徴をもつ。
その結果、
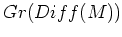 には「一つ次数がずれた」ブラケットが定義される。
このブラケットが、前節で定義された
には「一つ次数がずれた」ブラケットが定義される。
このブラケットが、前節で定義された 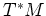 のシンプレクティック構造に
対応したポアソン括弧である。
のシンプレクティック構造に
対応したポアソン括弧である。
この対応から学ぶべきものはたくさんあるが、それはおいおいでて来るので、
ここではこのぐらいにとどめて先に進むことにする。
平成16年8月24日
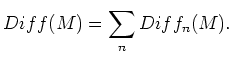
![]() のフィルトレーションは次のような特徴をもつ。
のフィルトレーションは次のような特徴をもつ。