

: の -表現 の正体
: 環 の -表現
: 有界性
まず、互いに可換な自己共役元
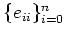 で生成される
で生成される 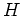 上の(可換)フォンノイマン環を考え、
その中のうまい射影 をとることにより、
上の(可換)フォンノイマン環を考え、
その中のうまい射影 をとることにより、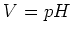 の元
の元 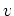 にたいし、
にたいし、
$i<j$ ならば
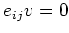
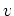 に対して、
だから、
に対して、
だから、
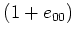 は可逆であるということに注意すると、
は可逆であるということに注意すると、
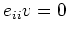
(for $i>0$) ゆえに
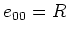
がなりたつ。
すなわち、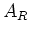 の表現では、
《最高ウエイトベクトル》が常に存在する。さらに、各
の表現では、
《最高ウエイトベクトル》が常に存在する。さらに、各 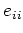 の有界性から、
がわかり、リー環の表現論の定石に従って
の有界性から、
がわかり、リー環の表現論の定石に従って 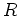 の整数性が導かれる。
の整数性が導かれる。
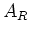 の関係式から、
の関係式から、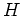 が《水増し》(同じもののいくつかの直和)
の違いを除いて一意に定まることはかなりやさしい。
が《水増し》(同じもののいくつかの直和)
の違いを除いて一意に定まることはかなりやさしい。
平成16年8月24日
![]() で生成される
で生成される ![]() 上の(可換)フォンノイマン環を考え、
その中のうまい射影 をとることにより、
上の(可換)フォンノイマン環を考え、
その中のうまい射影 をとることにより、![]() の元
の元 ![]() にたいし、
にたいし、