examples

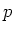
EXAMPLE 5.45   Let $k$ be a field of characteristic $p$ (possibly 0 ).

$$\mathfrak{gl}_n(k)$$

is a Lie algebra with the Killing form

$$\kappa_{\mathfrak{gl}_n(k)}(x,y)= \operatorname{tr}((\lambda(x)-\rho(x))(\lambda(y)-\rho(y)))$$

$$= \operatorname{tr}(\lambda(x y)) +\operatorname{tr}(\rho(x y)) -\operatorname{tr}(\lambda(x)\rho(y)-\operatorname{tr}(\lambda(y)\rho(x))$$

$$= 2n \operatorname{tr}(x y)-2 \operatorname{tr}(x)\operatorname{tr}(y).$$

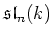$\mathfrak{sl}_n(k)$ is an ideal of 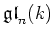$\mathfrak{gl}_n(k)$ and so its Killing form is given by

$$\kappa_{\mathfrak{sl}_n(k)}(x,y)=2 n\operatorname{tr}_{k^n}(x y).$$

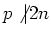
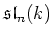
If $p \not \vert 2 n$ , then the Killing form is easily seen to be non-degenerate. so $\mathfrak{sl}_n(k)$ is a non-degenerated Lie algebra in this case. In this way we see that it is a semisimple Lie algebra. The Lie algebra is actually simple as we have shown in Proposition 5.22.

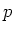
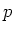
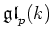
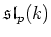
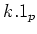
EXAMPLE 5.46   Let $p$ be an odd prime. Let $k$ be a field of characteristic $p$ . Then we have shown in Proposition 5.19 that the only non trivial ideals of $\mathfrak{gl}_p(k)$ are $\mathfrak{sl}_p(k)$ and $k.1_p$ . So we see that

$$L=\mathfrak{gl}_p(k)/k. 1_p$$

is a semisimple Lie algebra (as it has no proper abelian ideals). It has a unique nontrivial ideal

$$M=\mathfrak{sl}_p(k)/k. 1_p.$$

Thus $L$ cannot be a direct sum of simple Lie algebras.