We may assume that ![]() is an algebraically closed field.
is an algebraically closed field.
(1)
The composition
![]() is a representation of
is a representation of ![]() .
By Lemma 1.4 we see that
any irreducible sub representation of
.
By Lemma 1.4 we see that
any irreducible sub representation of ![]() is equivalent to
is equivalent to
![]() for some
for some
![]() .
By a dimensional argument, we conclude that
.
By a dimensional argument, we conclude that ![]() itself is equivalent to
itself is equivalent to
![]() . (In other words, there exists
. (In other words, there exists
![]() such that
such that
holds.) Thus
(2)
Let ![]() ,
, ![]() .
For any
.
For any
![]() , we have (using the same notation as above)
, we have (using the same notation as above)
Since we know by (1) that
Thus
![$\displaystyle [\phi(z),y]\in \bigcap_c \operatorname{Ker}(\Phi_c)=0.
$](img65.png)
So
Let
![]() be a
be a ![]() -algebra endomorphism of
-algebra endomorphism of ![]() .
Then by restriction we obtain a homomorphism
.
Then by restriction we obtain a homomorphism
Furthermore, if the base field
In precise, Let us write down
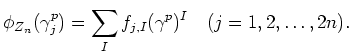
Then
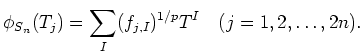
Here comes a geometric interpretation of endomorphisms of Weyl algebras.
| (*) | 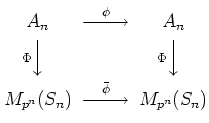 |
| (**) |
and
as in the previous Corollary. We put
We have an well-defined ![]() -algebra homomorphism
-algebra homomorphism
By using the isomorphism in , we obtain a
which is compatible with
It remains to prove that the map
![]() is represented as (**).
By pull-back, we obtain an
is represented as (**).
By pull-back, we obtain an ![]() -algebra homomorphism
-algebra homomorphism
Where the first isomorphism in the above line is the inverse of the following
by an argument similar to that in (I,Lemma 7.9), we see that
there exists
![]() such that
such that
holds. (See appendix for the detail.)
![]()