

: 付録
: 疑似指数 Q and A
: Q2.どのような基底の取り方をすれば、 と表せ、指数法則も成立 するのでしょうか?
A3.なります。本質的には 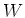 が
が
と、可算個で全体集合
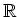 を分けていて、しかもそれぞれの
を分けていて、しかもそれぞれの 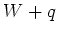 が
が 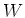 の
コピー(
の
コピー(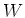 を平行移動したもの)であることに起因しています。
を平行移動したもの)であることに起因しています。
このことをきちんと示すにはルベーグ積分の知識が
必要ですから、ここではある程度その知識を仮定します。
以下、「可測」とは「ルベーグの意味で可測」という意味とし、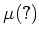 は
は 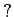 の
ルベーグ測度をあらわすこととします。
の
ルベーグ測度をあらわすこととします。
いま背理法で 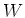 は可測であったと仮定します。
は可測であったと仮定します。
次の二つの補題を使います。
補題 3.1 (ルベーグ測度の平行移動不変性)
任意の可測集合
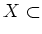
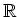
と 任意の実数
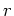
に対して、
この補題は、集合の測度が平行移動しても変わらないことを述べているので、
理解しやすいでしょう。
補題 3.2 (測度の可算加法性)
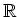
の可算個の可測集合
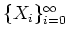
に対して、
(
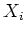
のどの二つも交わらないならば等号が成り立つ。)
この補題はルベーグ積分論で可算性がうまく用いられていることを
述べているもので、ルベーグ積分論の要の一つだと言えます。
さて、上の二つの補題を認めることにしますと、
もし 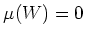 なら
なら
となって矛盾しますから、 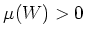 でなければならないことが分かります。
でなければならないことが分かります。
さらに、次の補題をもってきましょう。
補題 3.3 (
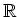
における測度と位相の関係)
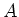
が
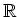
の可測集合で、
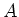
の測度が正である(つまり、0 でない)ならば、
は 0 の近傍を含む。
(ここでの
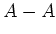
の定義は集合としての差
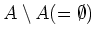
とは異なることに注意)
この補題の証明は、ルベーグ積分をどのように構成するかによって、議論のしかたが
変わってくるのですが、それを承知ですこしだけ説明をつけることにします。
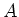 を次のように両端を切ったものの和集合で書きます。
を次のように両端を切ったものの和集合で書きます。
測度の可算加法性を思い出すと、ある正の整数 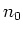 があって、
があって、
![$ A_0=A\cap [-n_0,n_0]$](img64.png) の測度も正であることがわかります。
の測度も正であることがわかります。
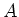 のところを
のところを 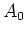 に減らしてやってなおかつ上の補題がなりたつならば、
もとの
に減らしてやってなおかつ上の補題がなりたつならば、
もとの 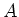 でも上の補題が成り立つのは明らかですから、
始めから
でも上の補題が成り立つのは明らかですから、
始めから 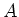 は有界である (とくに、その測度は有限である)と
仮定してよいことになります。
すると、
は
は有界である (とくに、その測度は有限である)と
仮定してよいことになります。
すると、
は 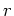 の連続関数3で、
の連続関数3で、
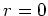 の時正の値をとります。ゆえに、ある
の時正の値をとります。ゆえに、ある
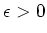 があって、
があって、
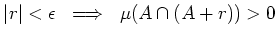 .
この
.
この 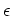 に対して、
というわけです。
に対して、
というわけです。
いま、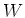 は
は
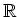 の
の
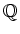 -部分空間だから、
-部分空間だから、
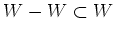 が成り立つということに注意して上の補題を使うと、
が成り立つということに注意して上の補題を使うと、
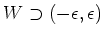 となる正の数
となる正の数 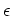 があることになります。
ところが下の補題を用いると、これは
があることになります。
ところが下の補題を用いると、これは
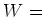
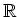 を意味して、矛盾というわけです。
を意味して、矛盾というわけです。
補題 3.4 (
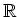
の 原点の近傍は(加法半群として)
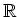
を生成する。)
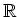
の部分集合
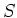
が次の二つの性質を持ったとする。
-
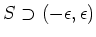 なる
なる
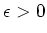 が存在する。
が存在する。
-
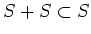
このとき、
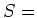
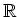
がなりたつ。
この補題自体の証明はとても簡単です。
(実は上に挙げた補題はいずれも位相群と呼ばれる対象の測度(Haar 測度)
や位相を調べる最初の道具としてつかわれる形に拡張できます。)
2002年10月9日
![]() が
が
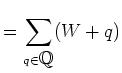
![]() は
は ![]() の
ルベーグ測度をあらわすこととします。
の
ルベーグ測度をあらわすこととします。
![]() は可測であったと仮定します。
は可測であったと仮定します。
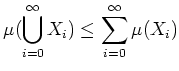
![]() なら
なら
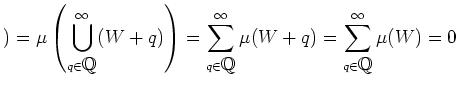
![]() を次のように両端を切ったものの和集合で書きます。
を次のように両端を切ったものの和集合で書きます。
![$\displaystyle A=\bigcup_{n\in \mathbb{N}} (A\cap [-n,n])
$](img62.png)
![]() は
は
![]() の
の
![]() -部分空間だから、
-部分空間だから、
![]() が成り立つということに注意して上の補題を使うと、
が成り立つということに注意して上の補題を使うと、
![]() となる正の数
となる正の数 ![]() があることになります。
ところが下の補題を用いると、これは
があることになります。
ところが下の補題を用いると、これは
![]()
![]() を意味して、矛盾というわけです。
を意味して、矛盾というわけです。