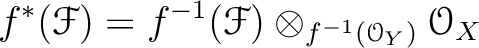Next: sheaves associated to modules Up: tensor products and inverse Previous: tensor products and localizations
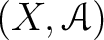 be a sheaf of algebras (possibly non commutative).
Let
be a sheaf of algebras (possibly non commutative).
Let
 be a right
be a right
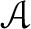 -module.
Let
-module.
Let
 be a left
be a left
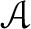 -module.
Then the tensor product
-module.
Then the tensor product
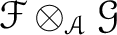 is the sheafication of the presheaf defined by
is the sheafication of the presheaf defined by
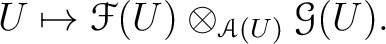
 be a morphism between locally ringed spaces.
Let
be a morphism between locally ringed spaces.
Let
 be a sheaf of
be a sheaf of
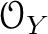 -modules on
-modules on 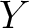 .
Then the inverse image of
.
Then the inverse image of
 as an
as an
 -module
with respect to
-module
with respect to  as
a sheaf of
as
a sheaf of
 -modules is defined as
-modules is defined as