Next: Definition of schemes Up: inverse images of sheaves Previous: inverse images of sheaves
 be a continuous map between topological spaces.
Let
be a continuous map between topological spaces.
Let
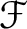 be a sheaf on
be a sheaf on 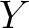 .
Then the inverse image
.
Then the inverse image
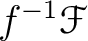 of
of
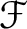 by
by 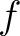 is
the sheafication of a presheaf
is
the sheafication of a presheaf
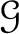 defined by
defined by
 be a continuous map between topological spaces.
Let
be a continuous map between topological spaces.
Let
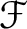 be a sheaf on
be a sheaf on 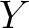 .
Then we have a natural isomorphism
.
Then we have a natural isomorphism
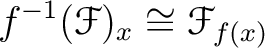
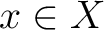 .
.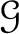 be the presheaf defined as in the previous Definition.
Since sheafication does not affect stalks, we have a natural isomorphism
be the presheaf defined as in the previous Definition.
Since sheafication does not affect stalks, we have a natural isomorphism
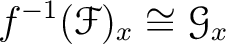
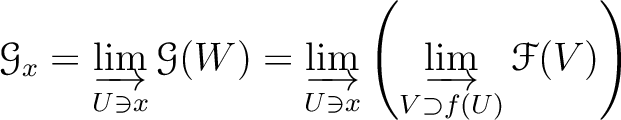
 is continuous, the injective limit at the right
hand side may be replaced by
is continuous, the injective limit at the right
hand side may be replaced by
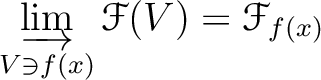
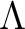
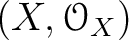 is a topological space
is a topological space 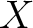 with a sheaf of rings
with a sheaf of rings
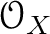 on it.
A locally ringed space is a ringed space whose stalks are local rings.
on it.
A locally ringed space is a ringed space whose stalks are local rings.
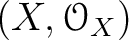
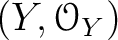 be ringed spaces.
be ringed spaces.
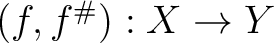 as ringed spaces
is a continuous map
as ringed spaces
is a continuous map  together
with a sheaf homomorphism
together
with a sheaf homomorphism
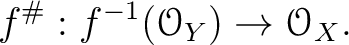
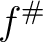 gives a ring homomorphism
gives a ring homomorphism
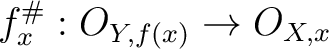
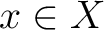 . We call it an “associated homomorphism”.)
. We call it an “associated homomorphism”.)
 are locally ringed space.
Then a morphism
are locally ringed space.
Then a morphism 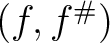 of ringed spaces is said to be
a morphism of locally ringed spaces
if the associated homomorphism
of ringed spaces is said to be
a morphism of locally ringed spaces
if the associated homomorphism 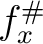 is a
local homomorphism for each point
is a
local homomorphism for each point 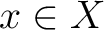 .
.
It goes without saying that when 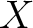 is a (locally) ringed space,
then its open set
is a (locally) ringed space,
then its open set 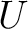 also carries a structure of (locally) ringed space
in a natural way, and that the inclusion map
also carries a structure of (locally) ringed space
in a natural way, and that the inclusion map  is a morphism
of (locally) ringed space.
is a morphism
of (locally) ringed space.