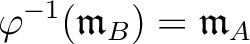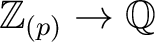Next: inverse images of sheaves Up: , , and the Previous: general localization of modules
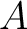 is said to be a local ring if it has only one
maximal ideal.
is said to be a local ring if it has only one
maximal ideal.
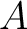 and for any prime ideal
and for any prime ideal
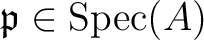 ,
the localization
,
the localization
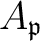 is a local ring with the maximal ideal
is a local ring with the maximal ideal
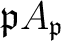 .
.
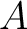 be a local ring. Then the maximal ideal of
be a local ring. Then the maximal ideal of 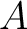 coincides with
coincides with
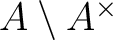 .
.
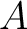 is a local ring if and only if
the set
is a local ring if and only if
the set
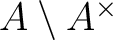 of non-units of
of non-units of 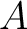 forms an ideal of
forms an ideal of 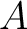 .
.
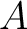 is a local ring with the maximal ideal
is a local ring with the maximal ideal
 .
Then for any element
.
Then for any element
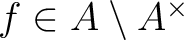 ,
an ideal
,
an ideal
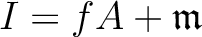 is an ideal of
is an ideal of 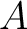 .
By Zorn's lemma, we know that
.
By Zorn's lemma, we know that 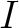 is contained in a maximal ideal of
is contained in a maximal ideal of 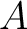 .
From the assumption, the maximal ideal should be
.
From the assumption, the maximal ideal should be
 .
Therefore, we have
.
Therefore, we have
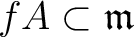
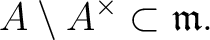
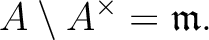
(2) The “only if” part is an easy corollary of (1). The “if” part is also easy.
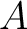 be a commutative ring. Let
be a commutative ring. Let
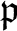 its prime ideal. Then
its prime ideal. Then
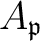 is
a local ring with the only maximal ideal
is
a local ring with the only maximal ideal
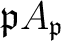 .
.
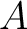 be a commutative ring. Let
be a commutative ring. Let
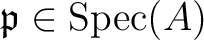 then the
stalk
then the
stalk
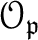 of
of
 on
on
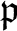 is isomorphic to
is isomorphic to
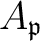 .
.
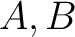 be local rings
with maximal ideals
be local rings
with maximal ideals
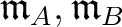 respectively.
A local homomorphism
respectively.
A local homomorphism
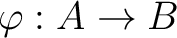 is a homomorphism which
preserves maximal ideals. That means, a homomorphism
is a homomorphism which
preserves maximal ideals. That means, a homomorphism 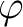 is said to be local
if
is said to be local
if