For example, the proof we gave in Theorem ![]() ,
especially the part where we chose the idempotent
,
especially the part where we chose the idempotent ![]() , was a bit complicated.
, was a bit complicated.
Let us give another proof using the sheaf arguments.
There exists a unique element
![]() which coincides with
which coincides with ![]() on
on ![]() and with 0
on
and with 0
on ![]() .
From the uniqueness we see that
.
From the uniqueness we see that
holds since
As a second easier example, we consider the following undergraduate problem.
Problem: Find the inverse of the matrix
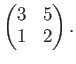
A student may compute (using ``operations on rows'') as follows.
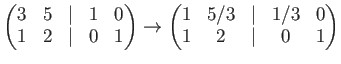 | ||
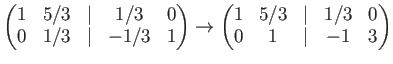 | ||
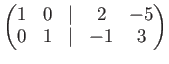 |
The calculation is valid on
![]() .
.
Another student may calculate (using ``operations on columns'') as follows.
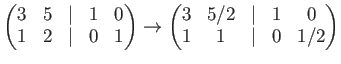 | ||
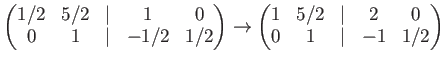 | ||
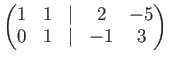 |
The calculation is valid on
![]() .
Of course, both calculations are valid on the intersection
.
Of course, both calculations are valid on the intersection
![]() .
.
The gluing lemma asserts that the answer obtained individually is automatically an answer on
the whole of
![]() .
Of course, in this special case, there are lots of easier ways to
tell that. But one may imagine this kind of thing is helpful when
we deal with more complicated objects.
.
Of course, in this special case, there are lots of easier ways to
tell that. But one may imagine this kind of thing is helpful when
we deal with more complicated objects.