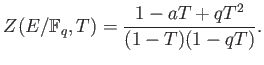Next: Bibliography
Zeta functions. No.4
Yoshifumi Tsuchimoto
PROPOSITION 4.1
Let
![% latex2html id marker 813
$ f\in \mathbb{F}_q[X]$](img1.png) be an irreducible polynomial in one variable of degree
be an irreducible polynomial in one variable of degree  .
Let us consider
.
Let us consider 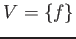 , an equation in one variable.
Then:
, an equation in one variable.
Then:
DEFINITION 4.2
Let
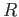
be a ring. A polynomial
![$ f(X_0,X_1,\dots,X_n)\in R[X_0,X_1,\dots, X_n]$](img8.png)
is said to be
homogenius of degree
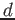
if an equality
holds as a polynomial in
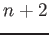
variables
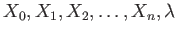
.
DEFINITION 4.3
Let
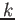
be a field.
- We put
and call it (the set of 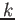 -valued points of) the projective space.
The class of an element
-valued points of) the projective space.
The class of an element
 in
in 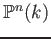 is
denoted by
is
denoted by
![$ [x_0:x_1:\dots:x_n]$](img16.png) .
.
- Let
![$ f_1,f_2,\dots, f_l \in k[X_0,\dots, X_n]$](img17.png) be homogenious polynomials. Then we set
be homogenious polynomials. Then we set
and call it (the set of 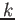 -valued point of) the projective variety
defined by
-valued point of) the projective variety
defined by
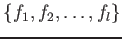 .
.
(Note that the condition
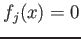
does not depend on the choice of the
representative
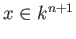
of
![$ [x]\in \P ^n(k)$](img22.png)
.)
LEMMA 4.4
We have the following picture of  .
.
That means, 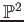 is divided into two pieces
is divided into two pieces
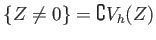 a
nd
a
nd
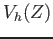 .
.
That means, 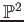 is covered by three ``open sets''
is covered by three ``open sets''
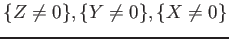 . Each of them is isomorphic to the
plane (that is, the affine space of dimension 2).
. Each of them is isomorphic to the
plane (that is, the affine space of dimension 2).
We quote the famous

It is a profound theorem, relating rational points
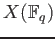 of
of 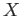 over finite fields
and topology of
over finite fields
and topology of
 .
.
The following proposition (which is a precursor of the above conjecture)
is a special case
PROPOSITION 4.6 (Weil)
Let 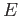 be an elliptic curve over
be an elliptic curve over
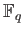 . Then we have
. Then we have
where 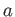 is an integer which satisfies
is an integer which satisfies
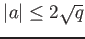 .
.
Note that for each 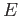 we have only one unknown integer
we have only one unknown integer 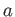 to
determine the Zeta function. So it is enough to compute
to
determine the Zeta function. So it is enough to compute
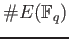 .
to compute the Zeta function of
.
to compute the Zeta function of 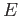 . (When
. (When 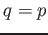 then one may use
the result in the preceding section.)
then one may use
the result in the preceding section.)
For a further study we recommend [1, Appendix C],[2].



Next: Bibliography
2015-05-09
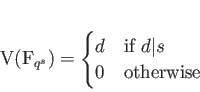
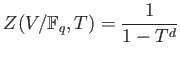
![]()
![]()
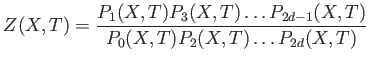
![]() of
of ![]() over finite fields
and topology of
over finite fields
and topology of
![]() .
.