


: 非可換スキームの定義
: 曲面の非可換変形のいくつかの例について
: 序説
目次
非可換空間の定義
非可換幾何学を始める上でまず問題になるのは、
非可換スキームというものをいかにして定義するかである。
ここでは Rosenberg [7] の見方を採用する事にする。
まず、「非可換空間」を定義する事から始めよう。
ここでは空間をその上の準連接層のなすアーベル圏によりとらえる。
すなわち非可換空間とはこの立場では単にアーベル圏のことである。
(層のセクションとは「場」の別名であると解釈できる。そう考えると
ここの考え方は空間をその上の場の「種類」と場の間の「関係」により
捉えようとしているとも言えて、なかなか面白い。)
非可換空間の間の射は次のようにして定義する。
Definition 2.1
[
7]
Let
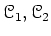
be abelian categories. A morphism
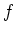
from
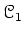
to
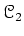
(in the sense of Rosenberg) is an isomorphness class of right exact
additive functors from
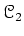
to
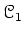
.
A representative of the class is called
an inverse image functor. And if we made a choice of one such,
we denote it by
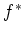
.
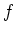
is said to be continuous if the inverse image
functor
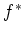
has a right adjoint (called a direct image functor
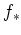
of
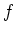
).
注意 右adjoint 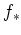 の存在は
の存在は
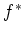 の順極限との可換性を保証している。
実際、
の順極限との可換性を保証している。
実際、
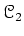 の任意の帰納系
の任意の帰納系 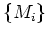 をとって来ると、
任意の
をとって来ると、
任意の
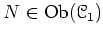 について、
について、
が成り立つから、
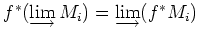 が
成り立つことが分かる。
上の定義で言うところの「連続」にはおそらくそういう意味がこめられている
のだろう。
が
成り立つことが分かる。
上の定義で言うところの「連続」にはおそらくそういう意味がこめられている
のだろう。
(適当なuniverseに関する)アーベル圏の全体に、上のようなmorphismを導入した物が、
我々の「非可換空間」のカテゴリーである。
もちろん、普通の意味のスキーム、環付き空間等々は、その上の準連接層を考える事
により、このカテゴリーの対象とみなす事ができる。
十分すぎるぐらい大きく見えるこの「空間」の捉え方にも
補うべき点があって、
1. 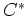 -代数の理論のような、環と加群に位相をもたせる理論では、
加群の全体はアーベル圏になり得ない。(同型でない全単射が存在したりする。)
このことは、例えば通常の環の
(ベクトル空間としての)双対を考えたい時などにはこれは少し問題になる。
(Manin [6] にも少しそのような位相の問題について
触れてある。)
-代数の理論のような、環と加群に位相をもたせる理論では、
加群の全体はアーベル圏になり得ない。(同型でない全単射が存在したりする。)
このことは、例えば通常の環の
(ベクトル空間としての)双対を考えたい時などにはこれは少し問題になる。
(Manin [6] にも少しそのような位相の問題について
触れてある。)
2. 定義できる限りは、正しくない(笑)。(1節をみよ)
そうは言うものの上の定義は代数的にはさしあたって考えられる限りいちばん大きな
風呂敷を広げていると言っても良いだろう。
ここまで空間の概念を広げておくと、
貼り合わせ等の諸概念についていちいち正当化の心配をしなくて済む。
安心感を与えてくれる定義である。
ところで、 ``準連接層の全体のカテゴリー''は、元の空間を復元できる
ぐらい十分多くのデータを持っているのか、と言う疑問が生じる。
結論から言えば、「構造射」をコミにして考えれば答えは肯定的である。
以下そのことについて述べることにしよう。
まず、(可換とは限らない)環 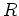 について、圏
について、圏
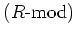 が
が 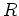 を復元できるかどうかについては、次の補題が答を与える。
を復元できるかどうかについては、次の補題が答を与える。
Lemma 2.1
Let
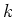
be a ring,
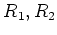
be
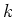
-algebras.
Let
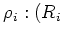
-
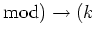
-

be structure morphisms (that is,
morphism defined by the structure homomorphisms
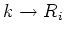
) (
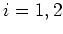
).
We define an equivalence of homomorphisms from
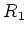
to
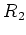
by saying that
two homomorphisms
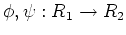
are equivalent if and only if
there exists an invertible
element
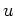
of
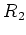
such that
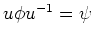
.
Then there is a bijection
between the set
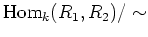
of equivalence classes
of k-algebra homomorphism and the set of
morphisms
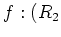
-
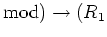
-

which satisfies
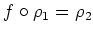
.
In particular, a category isomorphism
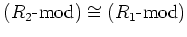
which commutes with
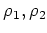
exists
if and only if
the two
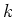
-algebras
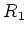
and
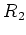
are isomorphic.
この補題の証明には、容易に分かる次の事実を使えば良い。
上の議論を追うと分かるのだが、
構造射 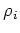 を指定する事には、
「基点」
を指定する事には、
「基点」
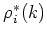 を決める役割がある。
実は
基点を決めないでおくと、
圏
を決める役割がある。
実は
基点を決めないでおくと、
圏
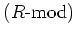 だけでは
だけでは 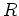 を同定するのに
十分な情報を与えない。
二つの環
を同定するのに
十分な情報を与えない。
二つの環 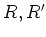 は
は
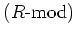 と
と
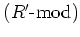 とが
圏として同値の時森田同値と言われる。ある環に森田同値な環
がどのようなものかについては次の補題でわかる。
とが
圏として同値の時森田同値と言われる。ある環に森田同値な環
がどのようなものかについては次の補題でわかる。
![]() の存在は
の存在は
![]() の順極限との可換性を保証している。
実際、
の順極限との可換性を保証している。
実際、
![]() の任意の帰納系
の任意の帰納系 ![]() をとって来ると、
任意の
をとって来ると、
任意の
![]() について、
について、
![]() -代数の理論のような、環と加群に位相をもたせる理論では、
加群の全体はアーベル圏になり得ない。(同型でない全単射が存在したりする。)
このことは、例えば通常の環の
(ベクトル空間としての)双対を考えたい時などにはこれは少し問題になる。
(Manin [6] にも少しそのような位相の問題について
触れてある。)
-代数の理論のような、環と加群に位相をもたせる理論では、
加群の全体はアーベル圏になり得ない。(同型でない全単射が存在したりする。)
このことは、例えば通常の環の
(ベクトル空間としての)双対を考えたい時などにはこれは少し問題になる。
(Manin [6] にも少しそのような位相の問題について
触れてある。)
![]() について、圏
について、圏
![]() が
が ![]() を復元できるかどうかについては、次の補題が答を与える。
を復元できるかどうかについては、次の補題が答を与える。
![]() を指定する事には、
「基点」
を指定する事には、
「基点」
![]() を決める役割がある。
実は
基点を決めないでおくと、
圏
を決める役割がある。
実は
基点を決めないでおくと、
圏
![]() だけでは
だけでは ![]() を同定するのに
十分な情報を与えない。
二つの環
を同定するのに
十分な情報を与えない。
二つの環 ![]() は
は
![]() と
と
![]() とが
圏として同値の時森田同値と言われる。ある環に森田同値な環
がどのようなものかについては次の補題でわかる。
とが
圏として同値の時森田同値と言われる。ある環に森田同値な環
がどのようなものかについては次の補題でわかる。