

: 有界性
: 環 の -表現
: 環 の生成元の満たす関係式
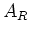 の
の 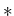 表現を考えるにあたって、
もともと、環
表現を考えるにあたって、
もともと、環 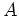 においては
であるから、
気分的には
においては
であるから、
気分的には 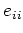 は正であることを仮定しても良いような気もする。
しかしこのことはわざわざ仮定しなくても必然的に出て来る。
この小節ではそのことを説明しよう。
は正であることを仮定しても良いような気もする。
しかしこのことはわざわざ仮定しなくても必然的に出て来る。
この小節ではそのことを説明しよう。
だから、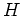 は二つのヒルベルト空間の直和である。
は二つのヒルベルト空間の直和である。
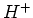 上では、
上では、
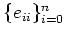 はそのことごとくが正値であり、
はそのことごとくが正値であり、
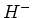 上では、
上では、
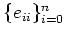 はそのことごとくが
はそのことごとくが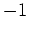 以下の作用素である。
と仮定したから、今の場合には
以下の作用素である。
と仮定したから、今の場合には 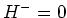 .
すなわち、
.
すなわち、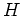 上で
である。
上で
である。
注意
本題からは外れるが、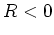 のときは逆に
である。このときには
のときは逆に
である。このときには
なる同型の存在によって、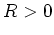 の場合に帰着できる。
の場合に帰着できる。
平成16年8月24日
![]() は二つのヒルベルト空間の直和である。
は二つのヒルベルト空間の直和である。
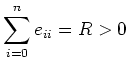
![]() のときは逆に
である。このときには
のときは逆に
である。このときには