

Next: 微分の公式いくつか
Up: 微分とは
Previous: 微分とは
実数上で定義された関数 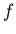 の微分について、
一応少しだけ書いておこう。その導入方法はいろいろあるが、
ここではやはり
の微分について、
一応少しだけ書いておこう。その導入方法はいろいろあるが、
ここではやはり 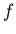 のグラフにこだわって、《
のグラフにこだわって、《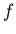 のグラフの、
のグラフの、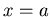 における
接線の傾き》と言う観点からみることにする。
における
接線の傾き》と言う観点からみることにする。
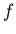 のグラフの接線を引くには、グラフ上の二点
のグラフの接線を引くには、グラフ上の二点 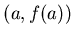 と
と
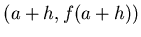 を結ぶ線の傾き
を結ぶ線の傾き
の 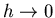 での極限を求めればよい。
(figure)
での極限を求めればよい。
(figure)
例によって、極限で
値を定義しようとするためには「その極限が本当に(ひとつに)定まるか?」
ということに注意を払う必要がある。(もちろん、極限が存在するかどうかは
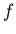 としてどのようなものをとるかに依存している。)この極限が存在する時、
《
としてどのようなものをとるかに依存している。)この極限が存在する時、
《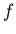 は
は 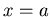 で微分可能である》と言い、
極限値(グラフの接線の傾きだね)のことを
で微分可能である》と言い、
極限値(グラフの接線の傾きだね)のことを
と書くんだ。
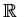 の各点で、
の各点で、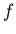 が微分可能なら、
が微分可能なら、
として、
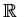 上の新しい関数
上の新しい関数 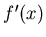 が定義できることにも注意しよう。
(プライム(
が定義できることにも注意しよう。
(プライム(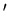 )がどこにつくかわかりにくい時には
)がどこにつくかわかりにくい時には
とも書く。もっとかんたんに、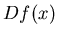 と書く時もある。)
と書く時もある。)
Yoshifumi Tsuchimoto
2000-04-12
![]() としてどのようなものをとるかに依存している。)この極限が存在する時、
《
としてどのようなものをとるかに依存している。)この極限が存在する時、
《![]() は
は ![]() で微分可能である》と言い、
極限値(グラフの接線の傾きだね)のことを
で微分可能である》と言い、
極限値(グラフの接線の傾きだね)のことを
![]() の各点で、
の各点で、![]() が微分可能なら、
が微分可能なら、