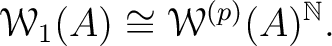Next: The ring of -adic Up: , , and the Previous: Playing with idempotents in
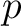 -adic Witt vectors (when the characteristic of the base ring
-adic Witt vectors (when the characteristic of the base ring
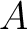 is
is 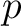 )
)
Before proceeding further, let me illustrate the idea.
Proposition 8.9 tells us an existence of
a set
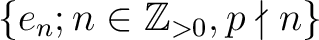 of
idempotents in
of
idempotents in
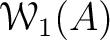 such that its order structure is
somewhat like the one found on the set
such that its order structure is
somewhat like the one found on the set
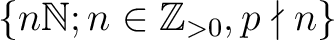 .
Knowing that the idempotents correspond to decompositions of
.
Knowing that the idempotents correspond to decompositions of
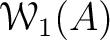 ,
we may ask:
,
we may ask:
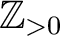 generated by the subsets
generated by the subsets
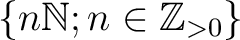 ?
?
To answer this problem, it would probably be better to find out,
for given positive number 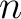 which is coprime to
which is coprime to 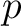 , what
the set
, what
the set
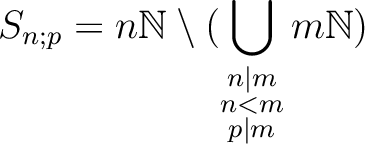
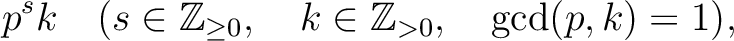
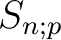 as above is equal to
as above is equal to
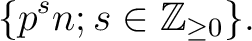
The answer to the problem is now given as follows:
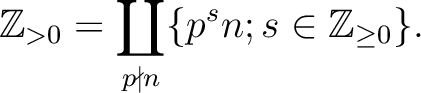
The same story applies to the ring
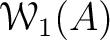 of universal Witt vectors for
a ring
of universal Witt vectors for
a ring 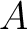 of characteristic
of characteristic 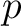 .
We should have a direct product expansion
.
We should have a direct product expansion
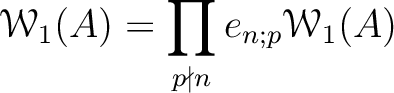
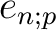 is defined by
is defined by
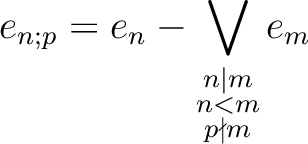
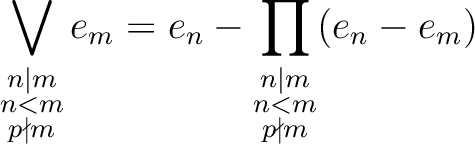
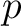 be a prime. Let
be a prime. Let 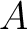 be an integral domain of characteristic
be an integral domain of characteristic 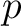 .
Let us define an idempotent
.
Let us define an idempotent 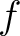 of
of
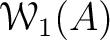 as follows.
as follows.
![$\displaystyle f=
\bigvee
_{\substack{
n>1\\
p \nmid n
}}
e_n
(=[1]-
\prod_
{\substack
{p \nmid n\\
n>1
}}
([1]- e_n))
$](img135.png)
Then  defines a direct product decomposition
defines a direct product decomposition
![$\displaystyle \mathcal W_1(A)
\cong
\left (
f \cdot \mathcal W_1(A)
\right )
\times
\left(
([1]- f)\cdot \mathcal W_1(A)
\right).
$](img136.png)
We call the factor algebra
![$([1] - f)\cdot \mathcal W_1(A)$](img137.png) the
ring
the
ring
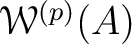 of
of 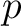 -adic Witt vectors.
-adic Witt vectors.
The following proposition tells us the importance of
the ring of 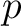 -adic Witt vectors.
-adic Witt vectors.
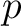 be a prime. Let
be a prime. Let 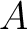 be a commutative ring of characteristic
be a commutative ring of characteristic 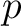 .
For each positive integer
.
For each positive integer 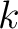 which is not divisible by
which is not divisible by 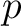 ,
let us define an idempotent
,
let us define an idempotent 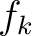 of
of
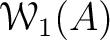 as follows.
as follows.
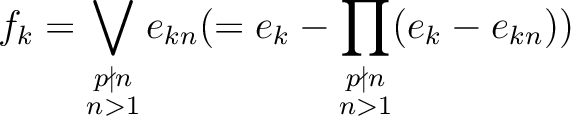
Then 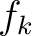 defines a direct product decomposition
defines a direct product decomposition
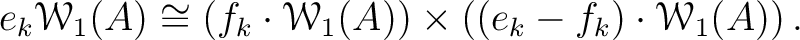
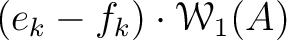 is isomorphic to the
ring
is isomorphic to the
ring
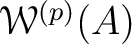 of
of 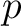 -adic Witt vectors.
Thus we have a direct product decomposition
-adic Witt vectors.
Thus we have a direct product decomposition